Bài 14 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao
LG a
Vectơ đối của vectơ \( - \overrightarrow a \) là vectơ nào?
Phương pháp giải:
Sử dụng định nghĩa véc tơ đối:
Nếu tổng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng \(\overrightarrow 0 \) thì ta nói \(\overrightarrow b \) là véc tơ đối của \(\overrightarrow a \).
Nghĩa là \(\overrightarrow a + \overrightarrow b = \overrightarrow 0 \) thì \(\overrightarrow b \) là véc tơ đối của \(\overrightarrow a \).
Lời giải chi tiết:
Vectơ đối của vectơ \( - \overrightarrow a \) là \( \overrightarrow a \) vì:
\( - \overrightarrow a + \overrightarrow a = \overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0 \)
LG b
Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ nào?
Lời giải chi tiết:
Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ \(\overrightarrow 0 \).
LG c
Vectơ đối của vectơ \(\overrightarrow a + \overrightarrow b \) là vectơ nào?
Lời giải chi tiết:
Vectơ đối của vectơ \(\overrightarrow a + \overrightarrow b \) là vectơ \( ( - \overrightarrow a)+( - \overrightarrow b) \) vì:
\(\begin{array}{l}
\overrightarrow a + \overrightarrow b + \left( { - \overrightarrow a } \right) + \left( { - \overrightarrow b } \right)\\
= \overrightarrow a + \left( { - \overrightarrow a } \right) + \overrightarrow b + \left( { - \overrightarrow b } \right)\\
= \overrightarrow 0 + \overrightarrow 0 \\
= \overrightarrow 0
\end{array}\)
Bài 15 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Chứng minh các mệnh đề sau đây
LG a
Nếu \(\overrightarrow a + \overrightarrow b = \overrightarrow c \) thì \(\overrightarrow a = \overrightarrow c - \overrightarrow b ,\overrightarrow b = \overrightarrow c - \overrightarrow a \)
Lời giải chi tiết:
Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow b \) ta có
\(\overrightarrow a + \overrightarrow b + \left( { - \overrightarrow b } \right) = \overrightarrow c + \left( { - \overrightarrow b } \right)\) \( \Rightarrow \overrightarrow a = \overrightarrow c - \overrightarrow b \)
Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow a \) ta có
\(\overrightarrow a + \overrightarrow b + \left( { - \overrightarrow a } \right) = \overrightarrow c + \left( { - \overrightarrow a } \right)\) \( \Rightarrow \overrightarrow b = \overrightarrow c - \overrightarrow a \)
LG b
\(\overrightarrow a - (\overrightarrow b + \overrightarrow c ) = \overrightarrow a - \overrightarrow b - \overrightarrow c \)
Phương pháp giải:
Sử dụng định nghĩa: Hiệu của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là tổng của véc tơ \(\overrightarrow a \) và véc tơ đối của \(\overrightarrow b \).
- Ta cần tính hiệu của \(\overrightarrow a \) và \((\overrightarrow b + \overrightarrow c )\) nên phải đi tìm véc tơ đối của \((\overrightarrow b + \overrightarrow c )\).
- Thực hiện cộng véc tơ \(\overrightarrow a\) với véc tơ vừa tìm được suy ra đpcm.
Lời giải chi tiết:
Véc tơ đối của \(\overrightarrow b + \overrightarrow c \) là \(\left( { - \overrightarrow b } \right) + \left( { - \overrightarrow c } \right)\) vì \(\overrightarrow b + \overrightarrow c + \left( { - \overrightarrow b } \right) + \left( { - \overrightarrow c } \right) = \overrightarrow 0 \)
Do đó
\(\overrightarrow a - \left( {\overrightarrow b + \overrightarrow c } \right) \) \(= \overrightarrow a + \left( { - \overrightarrow b } \right) + \left( { - \overrightarrow c } \right) \) \(= \overrightarrow a - \overrightarrow b - \overrightarrow c \)
LG c
\(\overrightarrow a - (\overrightarrow b - \overrightarrow c ) = \overrightarrow a - \overrightarrow b + \overrightarrow c \)
Phương pháp giải:
- Tìm véc tơ đối của \(\overrightarrow b - \overrightarrow c \).
- Thực hiện cộng véc tơ \(\overrightarrow a \) với véc tơ vừa tìm được suy ra đpcm.
Lời giải chi tiết:
Véc tơ đối của \(\overrightarrow b - \overrightarrow c \) là \(\left( { - \overrightarrow b } \right) + \overrightarrow c \) vì
\(\overrightarrow b - \overrightarrow c + \left( { - \overrightarrow b } \right) + \overrightarrow c \) \( = \overrightarrow b + \left( { - \overrightarrow c } \right) + \left( { - \overrightarrow b } \right) + \overrightarrow c = \overrightarrow 0 \)
Do đó
\(\overrightarrow a - \left( {\overrightarrow b - \overrightarrow c } \right)\) \( = \overrightarrow a + \left( { - \overrightarrow b } \right) + \overrightarrow c \) \( = \overrightarrow a - \overrightarrow b + \overrightarrow c \)
Bài 16 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho hình bình hành \(ABCD\) với tâm \(O\). Mỗi khẳng định sau đây đúng hay sai ?
LG a
\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {AB} \)
Phương pháp giải:
Sử dụng quy tắc ba điểm: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \)
Lời giải chi tiết:
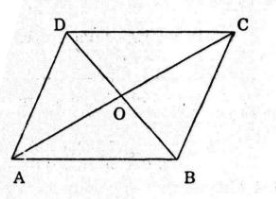
Sai vì \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \ne \overrightarrow {AB} .\)
LG b
\(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {BA} \)
Lời giải chi tiết:
Đúng vì:
ABCD là hình bình hành nên O là trung điểm AC.
Do đó \(\overrightarrow {CO} = \overrightarrow {OA} \). Khi đó,
\(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} .\)
LG c
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết:
Sai vì \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \ne \overrightarrow {AC} \).
LG d
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {BD} \)
Lời giải chi tiết:
Sai vì \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \ne \overrightarrow {BD} \).
LG e
\(\overrightarrow {CD} - \overrightarrow {CO} = \overrightarrow {BD} - \overrightarrow {BO} \)
Lời giải chi tiết:
Đúng vì \(\overrightarrow {CD} - \overrightarrow {CO} =\overrightarrow {OD} \) (quy tắc về hiệu véc tơ)
\( \overrightarrow {BD} - \overrightarrow {BO} = \overrightarrow {OD} \) (quy tắc về hiệu véc tơ)
Do đó, \(\overrightarrow {CD} - \overrightarrow {CO} = \overrightarrow {BD} - \overrightarrow {BO} \).
Bài 17 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho hai điểm \(A, B\) phân biệt.
LG a
Tìm tập hợp các điểm \(O\) sao cho \(\overrightarrow {OA} = \overrightarrow {OB} \)
Phương pháp giải:
Cộng cả hai vế với \(-\overrightarrow {OB}\).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\overrightarrow {OA} = \overrightarrow {OB} \\ \Leftrightarrow \overrightarrow {OA} + \left( { - \overrightarrow {OB} } \right) = \overrightarrow {OB} + \left( { - \overrightarrow {OB} } \right)\\ \Leftrightarrow \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {BA} = \overrightarrow 0 \\ \Leftrightarrow B \equiv A\end{array}\)
Do đó, \(\overrightarrow {OA} = \overrightarrow {OB} \) thì \(A \equiv B\) (A trùng B)
(vô lý do \(A, B\) phân biệt).
Vậy tập hợp điểm \(O\) thỏa mãn \(\overrightarrow {OA} = \overrightarrow {OB} \) là tập rỗng.
LG b
Tìm tập hợp các điểm \(O\) sao cho \(\overrightarrow {OA} = - \overrightarrow {OB} \).
Phương pháp giải:
Cộng cả hai vế với \(\overrightarrow {OB}\).
Lời giải chi tiết:
Ta có \(\overrightarrow {OA} = - \overrightarrow {OB} \)
\(\begin{array}{l}
\Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = - \overrightarrow {OB} + \overrightarrow {OB} \\
\Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0
\end{array}\)
\(\Leftrightarrow \,\,O\) là trung điểm đoạn \(AB\).
Vậy tập hợp điểm \(O\) thỏa mãn \(\overrightarrow {OA} = - \overrightarrow {OB} \) chỉ có duy nhất một điểm là trung điểm của đoạn \(AB\)
Bài 18 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho hình bình hành \(ABCD\). Chứng minh rằng \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \).
Lời giải chi tiết
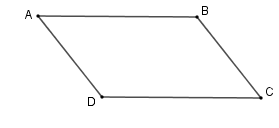
Ta có \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {BA} \)
Mà ABCD là hình bình hành nên \(\overrightarrow {BA} = \overrightarrow {CD} \)
Suy ra \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} \)
\( = \overrightarrow {BA} + \overrightarrow {DC} \)
\(= \overrightarrow {CD} + \overrightarrow {DC} \)
\(= \overrightarrow {CC}\)
\(= \overrightarrow 0 .\)
Bài 19 trang 18 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Chứng minh rằng \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau.
Lời giải chi tiết
Giả sử \(\overrightarrow {AB} = \overrightarrow {CD} \) và \(M, N\) lần lượt là trung điểm của \(AD,BC\).
Ta có \(\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 \)
\(\overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \)\( \Rightarrow - \overrightarrow {BN} - \overrightarrow {CN} = \overrightarrow 0 \)\(\Leftrightarrow - \left( {\overrightarrow {BN} + \overrightarrow {CN} } \right) = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {BN} + \overrightarrow {CN} = \overrightarrow 0 \)
và \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN}\)
\(\overrightarrow {MN} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} \)
Suy ra
\(\eqalign{
& 2\overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {MN} \cr&= \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} + \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} \cr
&= \left( {\overrightarrow {MA} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BN} + \overrightarrow {CN} } \right) + \overrightarrow {AB} + \overrightarrow {DC} \cr
& = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {AB} + \overrightarrow {DC} \cr&= \overrightarrow {AB} + \overrightarrow {DC} = \overrightarrow {AB} - \overrightarrow {CD} \cr
& = \overrightarrow 0 \cr} \)
Do đó, \(\overrightarrow {MN} = \overrightarrow 0 \) , tức là \(M \equiv N\).
Vậy trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau.
Ngược lại, ta giả sử trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau, suy ra
\(\overrightarrow {MA} + \overrightarrow {MD} = \overrightarrow 0 ,\,\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
Suy ra \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} \)\( = \overrightarrow {CM} + \overrightarrow {MD} = \overrightarrow {CD} \).
Cách khác:
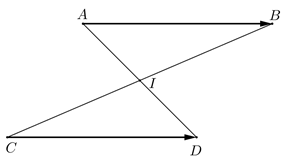
Ta chứng minh hai mệnh đề.
a) Cho \(\overrightarrow{AB}= \overrightarrow{CD}\) thì \(AD\) và \(BC\) có trung điểm trùng nhau.
Gọi \(I\) là trung điểm của \(AD\) ta chứng minh \(I\) cũng là trung điểm của \(BC\).
Theo quy tắc của ba điểm của tổng, ta có
\(\overrightarrow{AB}= \overrightarrow{AI} + \overrightarrow{IB}\);
\(\overrightarrow{CD}= \overrightarrow{CI}+ \overrightarrow{ID}\)
Vì \(\overrightarrow{AB} = \overrightarrow{CD}\) nên \(\overrightarrow{AI} + \overrightarrow{IB}= \overrightarrow{CI}+ \overrightarrow{ID}\)
\(\Rightarrow \overrightarrow{AI} - \overrightarrow{ID} = \overrightarrow{CI} - \overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{CI} + \overrightarrow{BI}\) (1)
Vì \(I\) là trung điểm của \(AD\) nên \(\overrightarrow {IA} + \overrightarrow {ID} = \overrightarrow 0 \Leftrightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\) (2)
Từ (1) và (2) suy ra \(\overrightarrow{CI} + \overrightarrow{BI} = \overrightarrow{0} \Leftrightarrow \overrightarrow {IC} + \overrightarrow {IB} = \overrightarrow 0 \) (3)
Đẳng thức (3) chứng tỏ \(I\) là trung điểm của \(BC\).
b) \(AD\) và \(BC\) có cùng trung điểm \(I\), ta chứng minh \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\).
\(I\) là trung điểm của \(AD\) \( \Leftrightarrow \overrightarrow {IA} + \overrightarrow {ID} = \overrightarrow 0 \Rightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\) \(\Rightarrow\overrightarrow{AI} - \overrightarrow{ID} =\overrightarrow{0}\)
\(I\) là trung điểm của \(BC\) \( \Leftrightarrow \overrightarrow {IC} + \overrightarrow {IB} = \overrightarrow 0 \) \(\Rightarrow \overrightarrow{CI} + \overrightarrow{BI}= \overrightarrow{0}\) \(\Rightarrow \overrightarrow{CI} - \overrightarrow{IB}= \overrightarrow{0}\)
Suy ra \(\overrightarrow{AI} - \overrightarrow{ID}= \overrightarrow{CI}- \overrightarrow{IB}\)
\(\Rightarrow \overrightarrow{AI} + \overrightarrow{IB} = \overrightarrow{CI}+ \overrightarrow{ID}\) \(\Rightarrow \overrightarrow{AB}= \overrightarrow{CD}\) (đpcm)
Chú ý:
Các em có thể trình bày ngắn gọn như sau:
Gọi \(M,N\) là trung điểm của \(AD,BC\) ta có: \(\overrightarrow {AM} = \overrightarrow {MD} ,\overrightarrow {BN} = \overrightarrow {NC} \)
Do đó,
\(\begin{array}{l}\overrightarrow {AB} = \overrightarrow {CD} \\ \Leftrightarrow \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NB} = \overrightarrow {CN} + \overrightarrow {NM} + \overrightarrow {MD} \\ \Leftrightarrow \left( {\overrightarrow {AM} - \overrightarrow {MD} } \right) + \left( {\overrightarrow {MN} - \overrightarrow {NM} } \right) + \left( {\overrightarrow {NB} - \overrightarrow {CN} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow 0 + \left( {\overrightarrow {MM} + \overrightarrow {MN} } \right) + \overrightarrow 0 = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MN} = \overrightarrow 0 \\ \Leftrightarrow M \equiv N\end{array}\)
Bài 20 trang 18 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho sáu điểm \(A, B, C, D, E, F\). Chứng minh rằng
\(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} \)\(= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} \)\(= \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \).
Lời giải chi tiết
Theo quy tắc ba điểm, ta có
\(\eqalign{
& \overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} \cr&= \left( {\overrightarrow {AE} + \overrightarrow {ED} } \right) + \left( {\overrightarrow {BF} + \overrightarrow {FE} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DF} } \right) \cr
&= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} + \left( {\overrightarrow {FE} + \overrightarrow {ED} + \overrightarrow {DF} } \right) \cr
&= \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} + \left( {\overrightarrow {FD} + \overrightarrow {DF} } \right) \cr
& = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} \cr} \)
Tương tự, ta cũng có
\(\eqalign{
& \overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} \cr&= \left( {\overrightarrow {AF} + \overrightarrow {FD} } \right) + \left( {\overrightarrow {BD} + \overrightarrow {DE} } \right) + \left( {\overrightarrow {CE} + \overrightarrow {EF} } \right) \cr
& = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} + \left( {\overrightarrow {FD} + \overrightarrow {DE} + \overrightarrow {EF} } \right) \cr
& = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} + \left( {\overrightarrow {FE} + \overrightarrow {EF} } \right) \cr
& = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \cr} \)
Vậy ta có \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD}\)\( = \overrightarrow {AF} + \overrightarrow {BD} + \overrightarrow {CE} \)
Cách khác:

Được cập nhật: 11 tháng 4 lúc 17:17:51 | Lượt xem: 377




