Bài tập ôn tập

Lý thuyết

Bài 1 trang 159 (Câu hỏi) SGK Đại số 10

Hãy phát biểu các khẳng định sau đây dưới dạng điều kiện cần và đủ.

Tam giác \(ABC\) vuông tại \(A\) thì \(BC^2= AB^2+AC^2\)

Tam giác \(ABC\) có các cách cạnh thỏa mãn hệ thức  \(BC^2 = AB^2+AC^2\) thì vuông tại \(A.\)

Hướng dẫn giải

Điều kiện cần và đủ của tam giác \(ABC\) vuông tại \(A\) là các cạnh của nó thỏa mãn hệ thức : \(c^2+ b^2 =a^2.\)

(với \(a,\, \, b,\, \, c\) là độ dài các cạnh theo thứ tự đối diện các đỉnh \(A,\, \,  B, \, \, C\)).

Bài 2 trang 159 SGK Đại số 10

Lập bảng biến thiên và vẽ đồ thị các hàm số.

a) \(y = -3x+2\)

b) \(y = 2x^2\)

c) \(y = 2x^2– 3x +1\)

Hướng dẫn giải

a) Bảng biến thiên

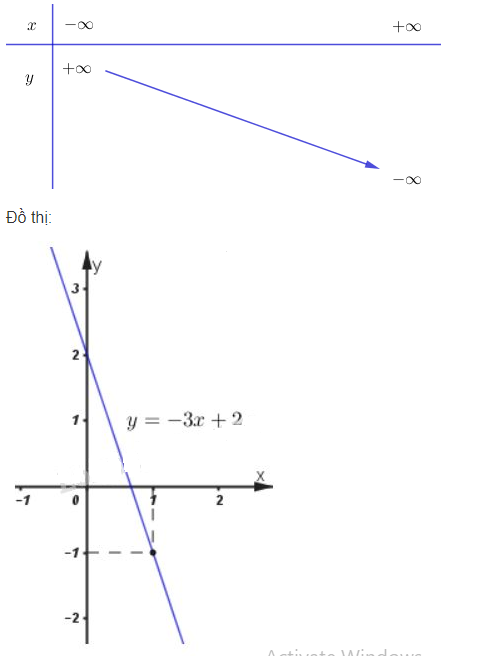
Đồ thị là đường thẳng đi qua \((0; 2)\) và \(({1; \, 1}).\)

b) Bảng biến thiên:

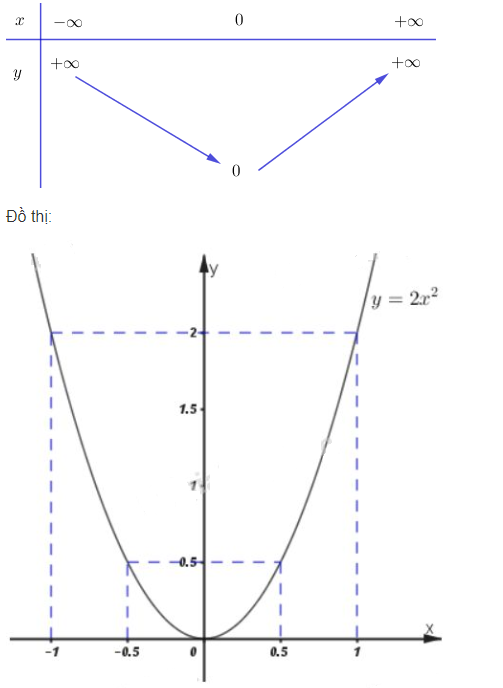
Đồ thị hàm số là đường cong đi qua các điểm \((0; \, 0), \, (-1; \, 2), \, (1;\, 2).\)

c) Bảng biến thiên

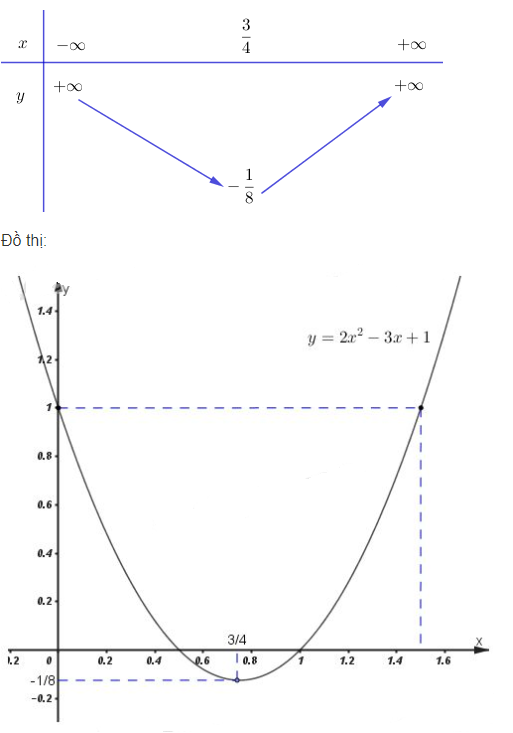
Đồ thị là parabol có đỉnh là \(I({3 \over 4},{{ - 1} \over 8})\) , trục đối xứng \(x = {3 \over 4}\) cắt trục tung tại \(P(0; 1)\), cắt trục hoành tại các điểm có hoành độ là nghiệm của phương trình:

 \(2{x^2} - 3x + 1 = 0 \Leftrightarrow {x_1} = {1 \over 2},{x_2} = 1\)

tức là cắt trục hoành tại \(({1 \over 2},0)\) và \((1;0).\)

Bài 3 trang 159 SGK Đại số 10

 Phát biểu quy tắc xét dấu một nhị thức bậc nhất. Áp dụng quy tắc đó để giải bất phương trình sau:

\(f(x) = {{(3x - 2)(5 - x)} \over {(2 - 7x)}} \ge 0.\)

Hướng dẫn giải

Ta có: 

\(\begin{array}{l}
+ )\;3x - 2 = 0 \Leftrightarrow x = \frac{2}{3}.\\
+ )\;5 - x = 0 \Leftrightarrow x = 5.\\
+ )\;2 - 7x = 0 \Leftrightarrow x = \frac{2}{7}.
\end{array}\)

Áp dụng: Ta lập bảng xét dấu của vế trái \(f(x)\) của bất phương trình:

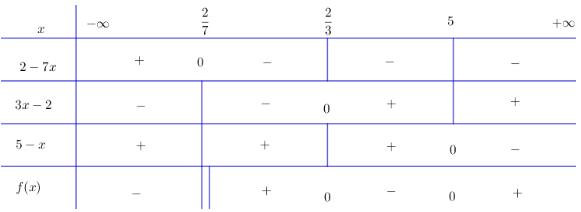
Tập nghiệm của bất phương trình: \(S = ({2 \over 7},{2 \over 3}{\rm{] }} \cup {\rm{ [}}5, + \infty )\)

Bài 4 trang 159 SGK Đại số 10

Phát biểu định lí về dấu của một tam thức bậc hai \(f(x) = ax^2+ bx + c\).

Áp dụng quy tắc đó, hãy xác định giá  trị của \(m\) để tam thức sau luôn luôn âm:  \(f(x) =  - 2{x^2} + 3x + 1 - m.\)  

Hướng dẫn giải

Định lí: Tam thức bậc hai \(f(x) = ax^2+ bx + c (a ≠0)\)

có biệt thức \(Δ = b^2– 4ac\)

- Nếu \(Δ < 0\) thì \(f(x)\) cùng dấu với hệ số \(a \) với mọi \(x∈\mathbb R\)

- Nếu \( Δ = 0\) thì \(f(x)\) luôn cùng dấu với hệ số \(a\) với mọi  \(x \ne {{ - b} \over {2a}}\)

- Nếu \(Δ >0\) thì \(f(x)\) có hai nghiệm \(x_1;x_2\) (\(x_1<x_2\))

    \( f(x)\) cùng dấu với hệ số \(a\) khi  \(x<x_1\) hoặc  \(x>x_2\)

     \(f(x)\) trái dấu với hệ số \(a\) khi  \(x_1<x<x_2\)

Áp dụng: \(f(x) =  - 2{x^2} + 3x + 1 - m\) có hệ số \(a = -2<0\)

Biệt thức: \(Δ = 3^2- 4 .(- 2) (1-m) = 17 - 8m\)

Ta có \(a=-2 < 0\) nên tam thức \(f(x)\) luôn âm (tức \(f(x) < 0 , ∀x  ∈\mathbb R\) khi:

\(\eqalign{
& \Delta < {\rm{ }}0 \Leftrightarrow 17 - 8m < 0 \cr 
& \Leftrightarrow m > {{17} \over 8}. \cr} \)

Bài 5 trang 159 SGK Đại số 10

Nêu các tính chất của bất đẳng thức. Áp dụng một trong các  tính chất đó, hãy so sánh các số \({2^{3000}}\) và \({3^{2000}}\).

Hướng dẫn giải

- Các tính chất của bất đẳng thức

TC1. ( Tính chất bắc cầu): \(\left\{ \matrix{A < B \hfill \cr B < C \hfill \cr} \right. \Rightarrow A < C\)

TC2. (Quy tắc cộng): \(A < B ⇔ A + C < B + C\)

TC3. (Quy tắc cộng hai bất đẳng thức dùng chiều) \(\left\{ \matrix{A < B \hfill \cr C < D \hfill \cr} \right. \Rightarrow A + C < B + D\)

TC4. (Quy tắc nhân): \(\left\{ \matrix{A < B \hfill \cr C > 0 \hfill \cr} \right. \Leftrightarrow AC < BC\)\(\left\{ \matrix{A < B \hfill \cr C < 0 \hfill \cr} \right. \Leftrightarrow AC > BC\)

TC5. (Quy tắc nhân hai bất đẳng thức): \(\left\{ \matrix{0 < A < B \hfill \cr 0 < C < D \hfill \cr} \right. \Rightarrow AC < B{\rm{D}}\)

TC6. (Quy tắc lũy thừa, khai căn)

Với \(A, B > 0, n ∈\mathbb N^*\) ta có:

                    \( A < B  \Leftrightarrow  A^n< B^n\)                     

                     \(A < B \Leftrightarrow \root n \of A  < \root n \of B \).

- Áp dụng tính chất: \(0<a^n<b^n\) với \(n∈ \mathbb N^*\)

\(\eqalign{
& {2^{3000}} = {\left( {{2^3}} \right)^{1000}} = {8^{1000}} \cr 
& {3^{2000}} = {\left( {{3^2}} \right)^{1000}} = {9^{1000}} \cr} \)

\(8<9\)

Do đó: \({2^{3000}} < {3^{2000}}.\)

Bài 8 trang 159 SGK Đại số 10

Nêu cách giải hệ hai phương trình bậc nhất hai ẩn và giải hệ: \(\left\{ \matrix{2x + y \ge 1 \hfill \cr x - 3y \le 1 \hfill \cr} \right.\)

Hướng dẫn giải

Áp dụng:

+ Để xác định miền nghiệm của bất phương trình \(2x + y ≥ 1\) ta dựng đường thẳng \((d): 2x + y = 1\) (tức là vẽ đồ thị hàm số \(y = -2x + 1\)).

Điểm \((0; 0) ∉ (d)\) ta có: \(2(0) + 0 < 1\).

Vậy nửa mặt phẳng bờ là \((d)\) không chứa điểm \((0; 0)\) là miền nghiệm của bất phương trình \(2x + y≥1\).

 + Tương tự, ta xác định miền nghiệm của bất phương trình \(x – 3y ≤ 1\).

Bài 1 trang 159 (Bài tập) SGK Đại số 10

Cho hàm số  \(f(x) = \sqrt {{x^2} + 3x + 4} \)\( - \sqrt { - {x^2} + 8x - 15} \)

a) Tìm tập xác định \(A\) của hàm số \(f(x)\)

b) Giả sử \(B = \left\{ {x \in R:4 < x \le \left. 5 \right\}} \right.\) . Hãy xác định các tập hợp \(A\backslash B\) và \(R\backslash (A\backslash B)\)

Hướng dẫn giải

a) Hàm số xác định  \( \Leftrightarrow \left\{ \begin{array}{l} {x^2} + 3x + 4 \ge 0\\- {x^2} + 8x - 15 \ge 0\end{array} \right.\) 

\( \Leftrightarrow \left\{ \begin{array}{l}
\forall x\; \in R\\
{x^2} - 8x + 15 \le 0
\end{array} \right.\\ \Leftrightarrow \left( {x - 3} \right)\left( {x - 5} \right) \le 0 \Leftrightarrow 3 \le x \le 5.\)

Vậy tập xác định của hàm số là: \(A = \left( {3;\;5} \right].\)

b) Ta có: \(B = \left\{ {x \in R|\;4 < x \le 5} \right\} = \left( {4;\;5} \right].\)

\(\Rightarrow A\backslash B = \left\{ {x|\;\;x \in A,\;\;x \notin B} \right\} \)\(= \left[ {3;\;4} \right].\)

\(\Rightarrow R\backslash \left( {A\backslash B} \right) = R\backslash \left[ {3;\;4} \right] = \left( { - \infty ;\;3} \right) \cup \)\(\left( {4;\; + \infty } \right).\)

Bài 2 trang 160 SGK Đại số 10

Cho phương trình: \(mx^2– 2x – 4m – 1 = 0\)

a) Chứng minh rằng với mọi giá trị \(m≠0\) phương trình đã cho có hai nghiệm phân biệt.

b) Tìm giá trị của \(m\) để \(- 1\) là một nghiệm của phương trình. Sau đó tìm nghiệm còn lại.

Hướng dẫn giải

\(mx^2– 2x – 4m – 1 = 0\)

\(\eqalign{& a) \, \Delta {\rm{ }} = {\rm{ }}1 + m\left( {4m + 1} \right) \cr&= 4{m^2} + m + 1 \cr & = (2m + {1 \over 4}) + {{15} \over {16}} > 0,\forall m \cr} \)

Vậy với \(m ≠ 0\) phương trình là bậc hai có biệt thức chung nên có \(2\) nghiệm phân biệt.

\(\eqalign{ b) 
& f( - 1) = m + 2 - 4m - 1 \cr&\;\;\;\;\;\;\;\;\;\;\,= - 3m + 1 = 0 \cr 
& \Rightarrow m = {1 \over 3} \cr} \)

Với \(m = {1 \over 3}\) , phương trình có nghiệm \(x_1= -1\).

Gọi nghiệm kia là \(x_2\).

Theo định lí Vi-et: 

\({x_1} + {x_2} =  - 1 + {x_2} = {2 \over m} = {2 \over {{1 \over 3}}}\)\( \Rightarrow {x_2} = 7\)

Bài 3 trang 160 SGK Đại số 10

Cho phương trình:  \({x^2} - 4mx + 9{(m - 1)^2} = 0\)

a) Xem xét với giá trị nào của \(m\), phương trình trên có nghiệm.

b) Giả sử \(x_1,x_2\) là hai nghiệm của phương trình đã cho, hãy tính tổng và tích của chúng. Tìm một hệ thức liên hệ giữa \(x_1\) và \(x_2\) không phụ thuộc vào \(m\).

c) Xác định \(m\) để hiệu các nghiệm của phương trình bằng \(4\).

Hướng dẫn giải

a) Phương trình có nghiệm  \(\Leftrightarrow Δ’ = 4m^2– 9(m-1) ^2\)\(= -5m^2+ 18m – 9 ≥ 0\)

 \(\Leftrightarrow {3 \over 5} \le m \le 3\)

Phương trình có nghiệm nếu \(m \in \left[ {{3 \over 5}; \, 3} \right]\)

b) Với  \(m \in \left[ {{3 \over 5},3} \right]\) phương trình có các nghiệm \(x_1,x_2\) thỏa mãn

\(x_1+x_2= 4m\) (1)  và   \(x_1.x_2= 9(m-1)^2\)   (2)

Từ (1) và (2) suy ra:

 \({x_1}.{x_2} = 9{({{{x_1} + {x_2}} \over 4} - 1)^2}\)

\(\Leftrightarrow 9{({x_1} + {x_2} - 4)^2} - 16{x_1}{x_2} = 0\)

Đó là hệ thức giữa hai nghiệm của phương trình độc lập với tham số \(m.\)

c) Không mất tính tổng quát, ta giả sử phương trình có hai nghiệm thỏa mãn: \(x_2 > x_1.\)

Khi đó ta có: \(x_2– x_1= 4;x_1+ x_2= 4m \)\(⇒ x_2= 2(m+1).\)

Thay biểu thức của \(x_2\) vào phương trình thì được:

\(4(m+1)^2 – 8m(m+1) + 9(m-1)^2\)\(= 0\)

\(\eqalign{
& \Leftrightarrow 5{m^2} - 18m + 13 = 0 \cr 
& \Leftrightarrow {m_{_1}} = 1;{m_2} = {{13} \over 5} \cr} \)

Kết luận: Nếu \(m = 1\) hoặc \(m = {{13} \over 5}\) thì hiệu của \(2\) nghiệm bằng \(4\).

Bài 4 trang 160 SGK Đại số 10

Chứng minh các bất đẳng thức:

a) \(5(x-1) < x^5– 1< 5x^4(x-1)\), biết \(x – 1 > 0\)

b) \(x^5+ y^5– x^4y – xy^4≥ 0\), biết \(x + y ≥ 0\)

c) \(\sqrt {4a + 1}  + \sqrt {4b + 1}  + \sqrt {4c + 1}  < 5\), biết rằng \(a, b, c\)  cùng lớn hơn \( - \frac{1}{4}\) và  \(a + b + c = 1.\)

Hướng dẫn giải

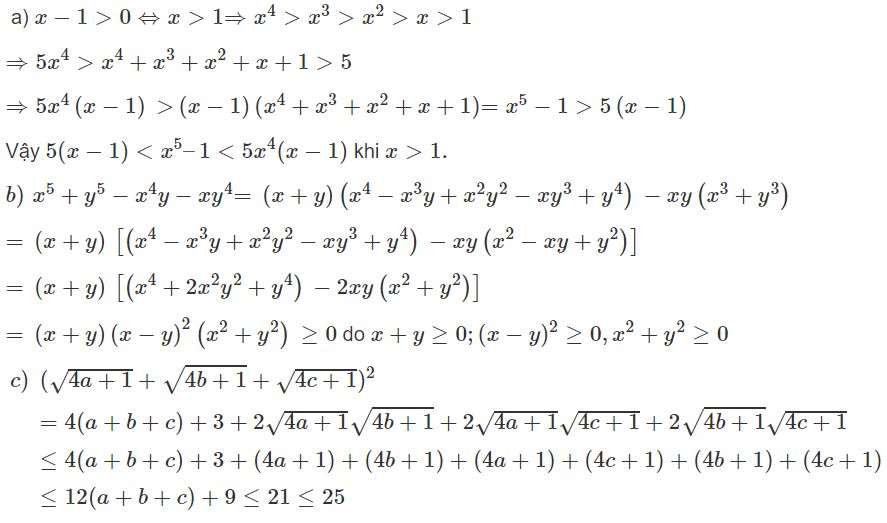
Suy ra Đpcm.

Bài 5 trang 160 SGK Đại số 10

Giải hệ phương trình sau bằng cách đưa về hệ phương trình dạng tam giác:

\(\left\{ \matrix{
x + 3y + 2z = 1 \hfill \cr 
3x + 5y - z = 9 \hfill \cr 
5x - 2y - 3z = - 3 \hfill \cr} \right.\)  (I)

Hướng dẫn giải

Ta có:

\(\begin{array}{l}
\;\;\;\;\left\{ \begin{array}{l}
3x + 5y - z = 9\\
x + 3y + 2z = 1\\
5x - 2y - 3z = - 3
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
6x + 10y - 2z = 18\\
x + 3y + 2z = 1\\
5x - 2y - 3z = - 3
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
7x + 13 = 19\\
x + 3y + 2z = 1\\
5x - 2y - 3z = - 3
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
7x + 13y = 19\\
3x + 9y + 6z = 3\\
10x - 4y - 6z = - 6
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
7x + 13y = 19\\
13x + 5y = - 3\\
10x - 4y - 6z = - 6
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
91x + 169y = 247\\
91x + 35y = - 21\\
10x - 4y - 6z = - 6
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
134y = 268\\
91x + 35y = - 21\\
10x - 4y - 6z = - 6
\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}
x = - 1\\
y = 2\\
x = - 2
\end{array} \right..
\end{array}\)

Vậy hệ phương trình có nghiệm \((x; y; z) = (-1; 2; -2).\)

Bài 6 trang 160 SGK Đại số 10

a) Xét dấu biểu thức: \(f(x) = 2x(x+2) – (x+2)(x+1).\)

b) Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc các đồ thị của các hàm số sau

\(y = 2x(x+2) (C_1)\) và \(y = (x+2)(x+1) (C_2).\)

Tính tọa độ các giao điểm \(A\) và \(B\) của \((C_1)\) và \((C_2)\)

c) Tính các hệ số \(a, b, c\) để hàm số \(y = ax^2+ bx + c\) có giá trị lớn nhất bằng \(8\) và đồ thị của nó đi qua \(A\) và \(B\).

Hướng dẫn giải

a)

\(\begin{array}{l}
f\left( x \right) = 2x\left( {x + 2} \right) - \left( {x + 2} \right)\left( {x + 1} \right)\\
= \left( {x + 2} \right)\left( {2x - x - 1} \right) \\= \left( {x + 2} \right)\left( {x - 1} \right).
\end{array}\)

Khi đó: 

\(\begin{array}{l}
f\left( x \right) \ge 0 \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) \ge 0\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x + 2 \ge 0\\
x - 1 \ge 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x + 2 \le 0\\
x - 1 \le 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \ge - 2\\
x \ge 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x \le - 2\\
x \le 1
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}
x \ge 1\\
x \le - 2
\end{array} \right..
\end{array}\) 

\(\begin{array}{l}
f\left( x \right) < 0 \Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) < 0\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x + 2 > 0\\
x - 1 < 0
\end{array} \right.\\
\left\{ \begin{array}{l}
x + 2 < 0\\
x - 1 > 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x > - 2\\
x < 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x < - 2\\
x > 1
\end{array} \right.
\end{array} \right.\\ \Leftrightarrow - 2 < x < 1.
\end{array}\)

Vậy \(f\left( x \right) \ge 0\) khi \(x \in \left( {0;\; - 2} \right] \cup \left[ {1; + \infty } \right).\)

\(f(x) < 0\) khi \(x \in \left( { - 2;\;1} \right).\)

b) Hàm số: \(y = 2x\left( {x + 2} \right) = 2{x^2} + 4x.\)

+) Tập xác định: R.

+) Đỉnh: \(\left( { - 1;\; - 2} \right).\)

+) Giao điểm của đồ thị hàm số với các trục tọa độ: \(\left( { - 2;\;0} \right),\;\left( {0;\;0} \right).\)

Ta có bảng biến thiên:

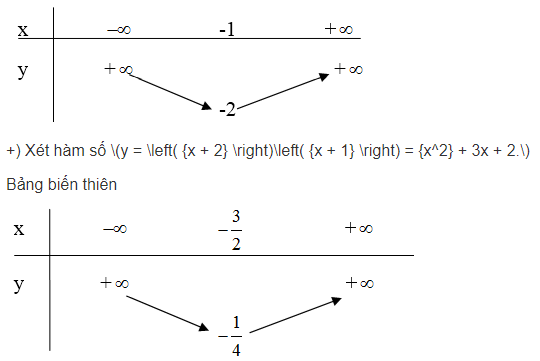
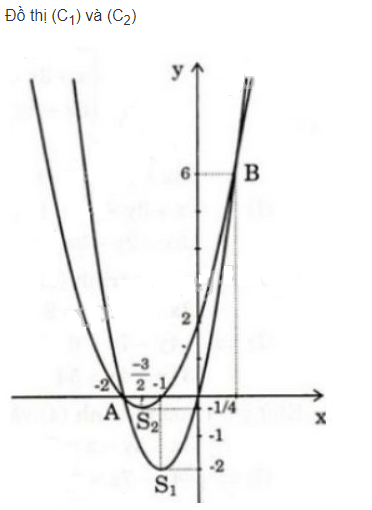
Hoành độ các giao điểm \(A\) và \(B\) của (C1) và (C2) là nghiệm của phương trình \(f(x) = 0  ⇔ x_1= -2, x_2= 1\)

\(⇔ A(-2; 0) , B(1; 6)\)

c) Theo đề bài ta có đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua A và B nên:

\(\left\{ \begin{array}{l}4x - 2b + c = 0\\a + b + c = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b - 2\\c = 8 - 2b\end{array} \right.\;\;\;\;\left( 1 \right).\)

Để hàm số \(y = a{x^2} + bx + c\) đạt giá trị lớn nhất bằng 8 thì:

\(\left\{ \begin{array}{l}a < 0\\\frac{{ - \Delta }}{{4a}} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\frac{{4ac - {b^2}}}{{4a}} = 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a < 0\\4ac - {b^2} = 32b\;\;\;\left( 2 \right)\end{array} \right.\)

Bài 7 trang 161 SGK Đại số 10

Chứng minh các hệ thức sau:

a) \({{1 - 2{{\sin }^2}a} \over {1 + \sin 2a}} = {{1 - \tan a} \over {1 + \tan a}}\)

b) \({{\sin a + \sin 3a + \sin 5a} \over {\cos a + \cos 3a + \cos 5a}} = \tan 3a\)

c) \({{{{\sin }^4}a - {{\cos }^4}a + {{\cos }^2}a} \over {2(1 - \cos a)}} = {\cos ^2}{a \over 2}\)

d) \({{\tan 2x\tan x} \over {\tan 2x - \tan x}} = \sin 2x\)

Hướng dẫn giải

\(\eqalign{ a) \, \, & {{1 - 2{{\sin }^2}a} \over {1 + \sin 2a}} \cr&= {{{{\cos }^2}a - {{\sin }^2}a} \over {{{\cos }^2}a + {{\sin }^2}a + 2\sin a\cos a}} \cr & = {{\cos a - \sin a} \over {\cos a + \sin a}} = {{1 - {{\sin a} \over {\cos a}}} \over {1 + {{\sin a} \over {\cos a}}}} \cr & = {{1 - \tan a} \over {1 + \tan a}} \cr} \)

\(\eqalign{b) \, \, 
& {{\sin a + \sin 3a + \sin 5a} \over {\cos a + \cos 3a + \cos 5a}} \cr 
& = {{2\sin {{a + 5a} \over 2}\cos {{5a - a} \over 2} + \sin 3a} \over {2\cos {{a + 5a} \over 2}\cos {{5a - a} \over 2} + \cos 3a}} \cr&= {{\sin 3a(1 + 2\cos 2a)} \over {\cos 3a(1 + 2\cos 2a)}} \cr 
& = \tan 3a \cr} \)

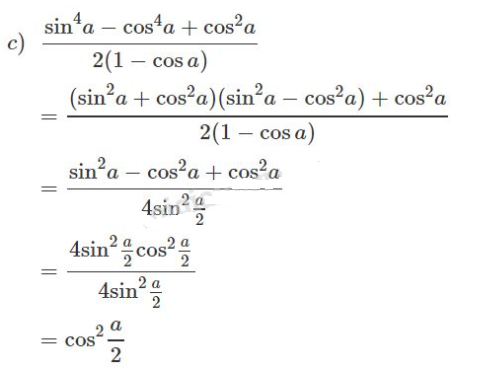
\(\eqalign{d)\, \, 
& {{\tan 2x\tan x} \over {\tan 2x - \tan x}} \cr 
& = {{{{2\tan x} \over {1 - {{\tan }^2}x}}.\tan x} \over {{{2\tan x} \over {1 - {{\tan }^2}x}} - \tan x}} \cr&= {{2\tan x} \over {{{\tan }^2}x + 1}} \cr 
& = \sin 2x \cr} \)

Bài 8 trang 161 SGK Đại số 10

Rút gọn các biểu thức sau:

a) \({{1 + \sin 4a - \cos 4a} \over {1 + \cos 4a + \sin 4a}}\)

b) \({{1 + \cos a} \over {1 - \cos a}}{\tan ^2}{a \over 2} - {\cos ^2}a\)

c) \({{\cos 2x - \sin 4x - \cos 6x} \over {\cos 2x + \sin 4x - \cos 6x}}\)

Hướng dẫn giải

\(\eqalign{a) \, \, & {{1 + \sin 4a - \cos 4a} \over {1 + \cos 4a + \sin 4a}} \cr&= {{2{{\sin }^2}2a + 2\sin 2a\cos 2a} \over {2{{\cos }^2}2a + 2\sin 2a\cos 2a}} \cr & = {{2\sin 2a(\sin 2a + \cos 2a)} \over {2\cos 2a(\sin 2a + \cos 2a)}} \cr&= \tan 2a \cr} \) 

\(\eqalign{b) \, \, 
& {{1 + \cos a} \over {1 - \cos a}}{\tan ^2}{a \over 2} - {\cos ^2}a\cr& = {{2{{\cos }^2}{a \over 2}} \over {2{{\sin }^2}{a \over 2}}}.{{2{{\sin }^2}{a \over 2}} \over {2{{\cos }^2}{a \over 2}}} - {\cos ^2}{a \over 2} \cr 
& = 1 - {\cos ^2}{a \over 2} = {\sin ^2}{a \over 2} \cr} \) 

\(\eqalign{c) \, \, 
& {{\cos 2x - \sin 4x - \cos 6x} \over {\cos 2x + \sin 4x - \cos 6x}} \cr&= {{(cos2x - \cos 6x) - sin4x} \over {(cos2x - \cos 6x) + sin4x}} \cr 
& = {{-2\sin {{2x + 6x} \over 2}\sin {{6x - 2x} \over 2} - \sin 4x} \over {-2\sin {{2x + 6x} \over 2}\sin {{2x - 6x} \over 2} + \sin 4x}} \cr 
& = {{2\sin 2x - 1} \over {2\sin 2x + 1}} \cr} \)

Bài 9 trang 161 SGK Đại số 10

Tính

a) \(4(cos{24^0} + \cos {48^0} - \cos {84^0} - \cos {12^0})\)

b) \(96\sqrt 3 \sin {\pi  \over {48}}\cos {\pi  \over {48}}\cos {\pi  \over {24}}\cos {\pi  \over {12}}\cos {\pi  \over 6}\)

c) \(\tan {9^0} - \tan {63^0} + \tan {81^0} - \tan {27^0}\)

Hướng dẫn giải

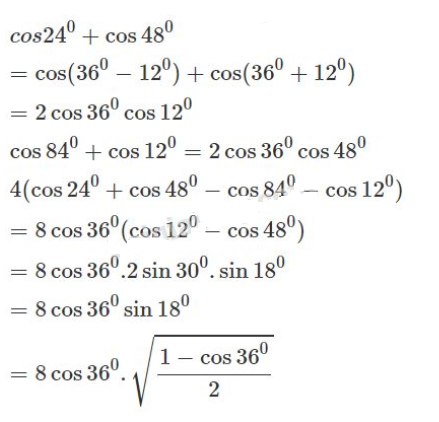
Đặt \(36^0= x\) ta có:

\(\eqalign{
& sin3x{\rm{ }} = {\rm{ }}sin{\rm{ }}\left( {{{180}^0} - 3x} \right) = sin2x \cr 
& \Leftrightarrow 3\sin x - 4{\sin ^3}x = 2\sin x\cos x \cr 
& \Leftrightarrow 3 - 4(1 - {\cos ^2}x) = 2{\mathop{\rm cosx}\nolimits} \cr 
& \Leftrightarrow 4co{s^2}x - 2\cos x - 1 = 0 \cr 
& \Rightarrow {\mathop{\rm cosx}\nolimits} = \cos {36^0} = {{1 + \sqrt 5 } \over 4} \cr} \)

Vậy : \(4(cos{24^0} + \cos {48^0} - \cos {84^0} - \cos {12^0}) \)\(= 2(1 + \sqrt 5 )\sqrt {{{3 - \sqrt 5 } \over 8}}  = 2\)

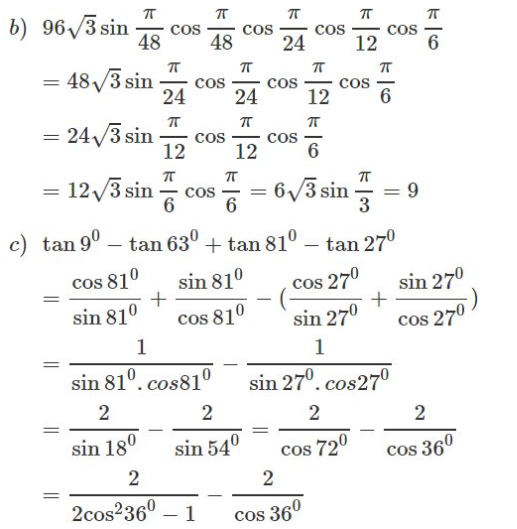
Thay  \(\cos {36^0} = {{1 + \sqrt 5 } \over 4}\) ta được: \(\tan {9^0} - \tan {63^0} + \tan {81^0} - \tan {27^0} \)\(= 4\)

Bài 10 trang 161 SGK Đại số 10

Rút gọn

a) \(\cos {x \over 5}\cos {{2x} \over 5}\cos {{4x} \over 5}\cos {{8x} \over 5}\)

b) \(\sin {x \over 7} + 2\sin {{3x} \over 7} + \sin {{5x} \over 7}\)

Hướng dẫn giải

a) Nhân biểu thức với \(\sin {x \over 5}\),ta có:

\(\eqalign{
& A\sin {x \over 5}\cr& = \sin {x \over 5}\cos {x \over 5}\cos {{2x} \over 5}\cos {{4x} \over 5}\cos {{8x} \over 5} \cr 
& = {1 \over 2}\sin {{2x} \over 5}\cos {{2x} \over 5}\cos {{4x} \over 5}\cos {{8x} \over 5} \cr 
& = {1 \over 4}\sin {{4x} \over 5}\cos {{4x} \over 5}\cos {{8x} \over 5} \cr&= {1 \over 8}\sin {{8x} \over 5}\cos {{8x} \over 5} \cr 
& = {1 \over {16}}\sin {{16x} \over 5} \cr} \)

Suy ra biểu thức rút gọn \(A =\sin{{16x} \over 5}:16\sin {x \over 5}.\)

b)

\(\eqalign{
& B = \sin {x \over 7} + 2\sin {{3x} \over 7} + \sin {{5x} \over 7}\cr& = 2\sin {{3x} \over 7} + (\sin {x \over 7} + \sin {{5x} \over 7}) \cr 
& = 2\sin {{3x} \over 7} \cr&\;\;\;+ 2\sin {1 \over 2}({{5x} \over 7} + {x \over 7})cos{1 \over 2}({{5x} \over 7} - {x \over 7}) \cr 
& = 2\sin {{3x} \over 7}(1 + \cos {{2x} \over 7}) \cr&= 4\sin {{3x} \over 7}{\cos ^2}{x \over 7}. \cr} \)

Bài 11 trang 161 SGK Đại số 10

Chứng minh rằng trong một tam giác \(ABC\) ta có:

a) \(\tan A + \tan B  +  \tan C \)\(= \tan A\tan B\tan C, \) \(\left( {\widehat A,\;\widehat B,\;\widehat C \ne \frac{\pi }{2}} \right).\)

b) \(\sin 2A + \sin 2B + \sin 2C \)\(= 4\sin A\sin B\sin C\)

Hướng dẫn giải

Bài 12 trang 161 SGK Đại số 10

Không sử dụng máy tính, hãy tính:

 \({{\sin {{40}^0} - \sin {{45}^0} + \sin {{50}^0}} \over {\cos {{40}^0} - \cos {{45}^0} + \cos {{50}^0}}} - {{6(\sqrt 3  + \tan {{15}^0})} \over {3 - \sqrt 3 \tan {{15}^0}}}\)

Hướng dẫn giải

Chú ý rằng:  \(sin{45^0} = {\rm{ }}cos{45^0},{\rm{ }}sin{40^0} = {\rm{ }}cos{50^0},\)\({\rm{ }}sin{50^0} = {\rm{ }}cos{40^0}\)

Ta được:

\({{\cos {{50}^0} - \cos {{45}^0} + \cos {{50}^0}} \over {\cos {{40}^0} - \cos {{45}^0} + \cos {{50}^0}}}- {{6.3({{\sqrt 3 } \over 3} + \tan {{15}^0})} \over {3(1 - {{\sqrt 3 } \over 3}\tan {{15}^0})}}\)

\(\eqalign{
& = 1 - 6({{\tan {{30}^0} + \tan {{15}^0}} \over {1 - \tan {{30}^0}.\tan {{15}^0}}}) \cr 
& = 1 - 6\tan {45^0} = - 5 \cr} \)