Bài 6 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Chứng minh rằng nếu \(\overrightarrow {AB} = \overrightarrow {CD} \) thì \(\overrightarrow {AC} = \overrightarrow {BD} \).
Phương pháp giải
Áp dụng quy tắc ba điểm: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết
Ta có:
\(\overrightarrow {AB} = \overrightarrow {CD} \)
\(\Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {CD} + \overrightarrow {BC} \) (cộng cả hai vế với \( \overrightarrow {BC} \))
\(\begin{array}{l}
\Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {BC} + \overrightarrow {CD} \\
\Leftrightarrow \overrightarrow {AC} = \overrightarrow {BD} \left( {dpcm} \right)
\end{array}\)
Cách khác:
\(\overrightarrow {AB} = \overrightarrow {CD} \)
\( \Leftrightarrow \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BD} \) (qui tắc ba điểm)
\(\overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {BC} = \overrightarrow {BD} + \overrightarrow {CB} + \overrightarrow {BC} \) (cộng cả hai vế với \(\overrightarrow {BC} \))
\(\begin{array}{l} \Leftrightarrow \overrightarrow {AC} + \overrightarrow 0 = \overrightarrow {BD} + \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {AC} = \overrightarrow {BD} \end{array}\).
Bài 7 trang 14 sách giáo khoa (SGK) Hình học 10 Nâng cao
Tứ giác \(ABCD\) là hình gì nếu \(\overrightarrow {AB} = \overrightarrow {DC} \) và \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)?
Lời giải chi tiết
Từ \(\overrightarrow {AB} = \overrightarrow {DC} \) suy ra \(ABCD\) là hình bình hành.
\(AB, BC\) là hai cạnh kề nhau của hình bình hành \(ABCD\) nên \(AB = BC\) thì \(ABCD\) là hình thoi.
(Hình bình hành có hai cạnh kề bằng nhau thì là hình thoi).
Bài 8 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho bốn điểm bất kì \(M, N, P, Q\). Chứng minh các đẳng thức sau
LG a
\(\overrightarrow {PQ} + \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MQ} \)
Phương pháp giải:
Sử dụng tính chất giao hoán và kết hợp của phép cộng véc tơ.
Quy tắc ba điểm: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
\(\overrightarrow {PQ} + \overrightarrow {NP} + \overrightarrow {MN} \)
\(= (\overrightarrow {MN} + \overrightarrow {NP} ) + \overrightarrow {PQ} \) (giao hoán)
\(= \overrightarrow {MP} + \overrightarrow {PQ} \) (quy tắc ba điểm)
\(= \overrightarrow {MQ} \) (quy tắc ba điểm)
LG b
\(\overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {QP} + \overrightarrow {MQ} \)
Lời giải chi tiết:
\(\overrightarrow {NP} + \overrightarrow {MN} \)
\(= (\overrightarrow {NQ} + \overrightarrow {QP} ) + (\overrightarrow {MQ} + \overrightarrow {QN} ) \) (quy tắc ba điểm)
\(= (\overrightarrow {QP} + \overrightarrow {MQ} ) +( \overrightarrow {NQ} + \overrightarrow {QN} ) \) (giao hoán)
\(= \overrightarrow {QP} + \overrightarrow {MQ} \) (quy tắc ba điểm)
( vì \(\overrightarrow {NQ} + \overrightarrow {QN} = \overrightarrow 0 \) )
Cách khác:
\(\begin{array}{l}\overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} \\ = \overrightarrow {MP} \,\,\,\,\left( 1 \right)\\\overrightarrow {QP} + \overrightarrow {MQ} = \overrightarrow {MQ} + \overrightarrow {QP} \\ = \overrightarrow {MP} \,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) suy ra \(\overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {QP} + \overrightarrow {MQ} \).
LG c
\(\overrightarrow {MN} + \overrightarrow {PQ} = \overrightarrow {MQ} + \overrightarrow {PN} \)
Lời giải chi tiết:
\(\overrightarrow {MN} + \overrightarrow {PQ}\)
\( = (\overrightarrow {MQ} + \overrightarrow {QN} ) + (\overrightarrow {PN} + \overrightarrow {NQ} ) \)
\(= \overrightarrow {MQ} + \overrightarrow {PN} + \overrightarrow {QN} + \overrightarrow {NQ} \)
\(= \overrightarrow {MQ} + \overrightarrow {PN} \)
(vì \(\overrightarrow {QN} + \overrightarrow {NQ} = \overrightarrow {QQ} = \overrightarrow 0 \))
Bài 9 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Các hệ thức sau đây đúng hay sai (với mọi \(\overrightarrow a \) và \(\overrightarrow b \) )?
LG a
\(\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Phương pháp giải:
Chứng minh \(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\) bằng cách dựng hình và sử dụng bất đẳng thức tam giác.
Từ đó suy ra tính đúng sai của mỗi câu.
Lời giải chi tiết:
Ta sẽ chứng minh \(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Chứng minh:
Từ một điểm \(O\) trong mặt phẳng ta dựng vectơ:
\(\eqalign{
& \overrightarrow {OA} = \overrightarrow a \cr
& \overrightarrow {OB} = \overrightarrow b \cr} \)
Và dựng hình bình hành \(OACB\) \( \Rightarrow \overrightarrow {AC} = \overrightarrow {OB} \)
Như vậy:
\(\eqalign{
& OA = |\overrightarrow {OA} | = |\overrightarrow a | \cr
& OB = |\overrightarrow {OB} | = |\overrightarrow b | \cr&\Rightarrow AC = |\overrightarrow {AC} |=|\overrightarrow {OB} | = |\overrightarrow b | \cr
& \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \Rightarrow \overrightarrow {OC} = \overrightarrow a + \overrightarrow b \cr
& OC = |\overrightarrow {OC} | = |\overrightarrow a + \overrightarrow b | \cr} \)
Áp dụng bất đẳng thức tam giác vào tam giác \(OAC\), ta có:
\(OA + AC ≥ OC \) \(\Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \ge \left| {\overrightarrow a + \overrightarrow b } \right|\)
\( ⇒ |\overrightarrow a + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow {b|} \).
Dấu "=" xảy ra khi OA+AC=OC hay A nằm giữa O và C.
Khi đó \(\overrightarrow {OA} ,\overrightarrow {AC} \) cùng hướng hay \(\overrightarrow a ,\overrightarrow b \) cùng hướng. (Do \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b \))
Chú ý:
Các em cũng không nhất thiết phải dựng hình bình hành. Có thể dựng hình cách khác như sau:
Từ điểm O dựng điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \).
Từ điểm A dựng điểm C sao cho \(\overrightarrow {AC} = \overrightarrow b \).
Rồi sử dụng bất đẳng thức tam giác cũng ra được đpcm.
Do đó a sai.
LG b
\(\left| {\overrightarrow a + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)
Lời giải chi tiết:
Đúng.
Bài 10 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho hình bình hành \(ABCD\) với tâm \(O\). Hãy điền vào chỗ trống (…) để được đẳng thức đúng
LG a
\(\overrightarrow {AB} + \overrightarrow {AD} = ....\)
Phương pháp giải:
Sử dụng quy tắc ba điểm, quy tắc hình bình hành:
Với ba điểm M, N, P bất kì ta có: \(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \)
Nếu OABC là hình bình hành thì ta có:
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} \)
Lời giải chi tiết:
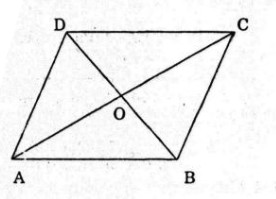
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành).
LG b
\(\overrightarrow {AB} + \overrightarrow {CD} = ......\)
Lời giải chi tiết:
\(\overrightarrow {AB} + \overrightarrow {CD} = \,\overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow {AA} = \overrightarrow 0 \,\)
LG c
\(\overrightarrow {AB} + \overrightarrow {OA} = ......\)
Lời giải chi tiết:
\(\overrightarrow {AB} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AB} \) (giao hoán)
\( = \overrightarrow {OB} \) (quy tắc ba điểm)
LG d
\(\overrightarrow {OA} + \overrightarrow {OC} = .......\)
Lời giải chi tiết:
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) (vì O là trung điểm của AC).
LG e
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = ........\)
Lời giải chi tiết:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
\(= (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} ) \) (giao hoán)
\(= \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)
(vì O là trung điểm của AC).
Bài 12 trang 14 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\).
LG a
Hãy xác định các điểm \(M, N, P\) sao cho
\(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \,;\)
\(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \,;\)
\(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \)
Lời giải chi tiết:

\(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) \( \Leftrightarrow \) M là đỉnh còn lại của hình bình hành AOBM.
AOBM là hình bình hành ⇒ AM//BO
\(\begin{array}{l} \Rightarrow \widehat {MAO} + \widehat {AOB} = {180^0}\\ \Leftrightarrow \widehat {MAO} + {120^0} = {180^0}\\ \Rightarrow \widehat {MAO} = {60^0}\end{array}\)
Ta có: \(\widehat {MAO} = {60^0},\widehat {OAC} = {30^0}\) \( \Rightarrow \widehat {MAC} = \widehat {MAO} + \widehat {OAC}\) \( = {60^0} + {30^0} = {90^0}\)
\( \Rightarrow MA \bot AC\)\( \Rightarrow CM\) là đường kính của đường tròn tâm O.
Vậy điểm \(M\) là điểm sao cho \(CM\) là đường kính của đường tròn tâm \(O\).
Tương tự, ta cũng có \(N, P\) thuộc đường tròn \((O)\) sao cho \(AN, BP\) là đường kính của đường tròn \((O)\).
Cách khác:
Kéo dài \(OC\) cắt đường tròn tại điểm \(M\).
MC là đường kính nên \(\widehat {MBC} = {90^0} \Rightarrow MB \bot BC\).
Mà tam giác ABC đều nên \(AO\bot BC\).
Do đó MB//OA (1)
Lại có \(\widehat {MAC} = {90^0} \Rightarrow MA \bot AC\).
Mà tam giác ABC đều nên \(BO\bot AC\).
Do đó MA//BO (2)
Từ (1) và (2) suy ra \(OAMB\) là hình bình hành, suy ra:
\(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OM} \).
Vậy M là điểm cần tìm.
LG b
Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \).
Lời giải chi tiết:

\(O\) là trung điểm của \(MC\) nên \(\overrightarrow {OM} + \overrightarrow {OC} = \overrightarrow 0 \), mà \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0 \)
Bài 13 trang 15 Sách giáo khoa (SGK) Hình học 10 Nâng cao
Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt tại \(O\) (h.17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau

LG a
\(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều có cường độ là \(100N\), góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({120^0}\) (h.17a)
Phương pháp giải:
- Sử dụng quy tắc hình bình hành dựng véc tơ tổng hợp lực.
- Sử dụng kiến thức hình học phẳng tính độ dài đoạn thẳng.
Lời giải chi tiết:

Ta lấy \(\overrightarrow {{F_2}} = \overrightarrow {OA} ,\,\overrightarrow {{F_1}} = \overrightarrow {OB} \).
Theo quy tắc hình bình hành, ta vẽ hình bình hành \(OACB\).
Hình bình hành \(OACB\) có \(OA = OB\) nên \(OACB\) là hình thoi.
Ta có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \), \(OC\) là phân giác góc \(\widehat {AOB}\) nên \(\widehat {AOC} = {60^0}\).
Mà \(OACB\) là hình thoi nên OA=AC hay tam giác \(AOC\) đều.
Suy ra \(OA = OC\).
Vậy cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(100N\).
LG b
Cường độ của \(\overrightarrow {{F_1}} \) là \(40N\), của \(\overrightarrow {{F_2}} \) là \(30N\) và góc giữa \(\overrightarrow {{F_1}} \) và \( \overrightarrow {{F_2}} \) bằng \(90^0\)(h.17b)
Lời giải chi tiết:

Đặt \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} \). \(C\) là đỉnh thứ tư của hình bình hành \(OACB\).
Do góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({90^0}\) suy ra tứ giác \(OACB\) là hình chữ nhật.
Ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Theo pitago trong tam giác OAC có:
\(OC = \sqrt {O{A^2} + A{C^2}} = \sqrt {O{A^2} + O{B^2}}\)
\( = \sqrt {{{40}^2} + {{30}^2}} \) \( = 50N\)
Vậy cường độ tổng hợp lực của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(50N.\)
Được cập nhật: 21 tháng 4 lúc 4:13:39 | Lượt xem: 417




