Bài 4 trang 51 SGK Hình học 10 nâng cao
Trong các trường hợp nào tích vô hướng \(\overrightarrow a .\overrightarrow b \) có giá trị dương, có giá trị âm, bằng \(0\) ?
Lời giải chi tiết
Ta có:
\(\begin{array}{l}
\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\\
\left| {\overrightarrow a } \right| > 0,\left| {\overrightarrow b } \right| > 0\\
+ )\overrightarrow a .\overrightarrow b > 0 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) > 0\\
\Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) < {90^0}\\
+ )\overrightarrow a .\overrightarrow b < 0 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) < 0\\
\Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) > {90^0}\\
\overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 0\\
\Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {90^0}
\end{array}\)
Vậy,
Tích vô hướng của hai vecto là số dương khi góc giữa hai vecto nhỏ hơn 90o.
Tích vô hướng của hai vecto là số âm khi góc giữa hai vecto lớn hơn 90o.
Tích vô hướng của hai vecto bằng 0 khi góc giữa hai vecto bằng 90o.
Bài 5 trang 51 SGK Hình học 10 nâng cao
Cho tam giác \(ABC\). Tổng \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) + (\overrightarrow {BC} ,\,\overrightarrow {CA} ) + (\overrightarrow {CA} ,\,\overrightarrow {AB} )\) có thể nhận giá trị nào trong các giá trị sau : \({90^0}\,;\,{180^0}\,;\,{270^{0\,}}\,;\,{360^0}\) ?
Lời giải chi tiết
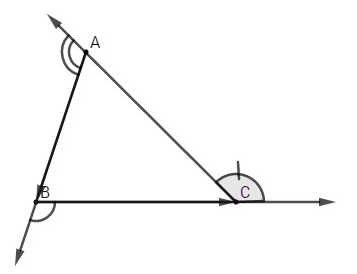
Ta có
\((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {180^0} - \widehat B\) vì góc \((\overrightarrow {AB} ,\,\overrightarrow {BC} )\) và \(\widehat B\) là hai góc kề bù.
\((\overrightarrow {BC} ,\,\overrightarrow {CA} ) = {180^0} - \widehat C\) vì góc \((\overrightarrow {BC} ,\,\overrightarrow {CA} )\) và \(\widehat C\) là hai góc kề bù.
\((\overrightarrow {CA} ,\,\overrightarrow {AB} ) = {180^0} - \widehat A\) vì góc \((\overrightarrow {CA} ,\,\overrightarrow {AB} )\) và \(\widehat A\) là hai góc kề bù.
Do đó \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) + (\overrightarrow {BC} ,\,\overrightarrow {CA} ) + (\overrightarrow {CA} ,\,\overrightarrow {AB} ) \)
\(\begin{array}{l}
= {180^0} - \widehat B + {180^0} - \widehat C + {180^0} - \widehat A\\
= {540^0} - \left( {\widehat B + \widehat C + \widehat A} \right)\\
= {540^0} - {180^0}\\
= {360^0}
\end{array}\)
Bài 6 trang 51 SGK Hình học 10 nâng cao
Cho tam giác \(ABC\) vuông ở \(A\) và \(\widehat B = {30^0}\). Tính giá trị của các biểu thức sau
LG a
\(\cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2}\)
Phương pháp giải:
Xác định góc giữa các véc tơ đã cho và giá trị lượng giác của chúng.
Từ đó thay vào tính giá trị biểu thức.
Lời giải chi tiết:

Ta có: \(\widehat B = {30^0} \) \(\Rightarrow \widehat C = {90^0} - {30^0} = {60^0}\)
\((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {150^0};(\overrightarrow {BA} ,\,\overrightarrow {BC} ) = {30^0},\) \((\overrightarrow {AC} ,\,\overrightarrow {CB} ) = {120^0}\)
Do đó
\(\eqalign{
& \cos (\overrightarrow {AB} ,\,\overrightarrow {BC} ) + \sin (\overrightarrow {BA} ,\,\overrightarrow {BC} ) + \tan {{(\overrightarrow {AC} ,\,\overrightarrow {CB} )} \over 2}\cr& = \cos {150^0} + {\mathop{\rm s}\nolimits} {\rm{in3}}{{\rm{0}}^0} + \tan {60^0} \cr
& = {{ - \sqrt 3 } \over 2} + {1 \over 2} + \sqrt 3 = {{\sqrt 3 + 1} \over 2} \cr} \)
LG b
\(\sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} )\)
Lời giải chi tiết:
Ta có \((\overrightarrow {CA} ,\,\overrightarrow {BA} ) = {90^0}\), do đó
\(\eqalign{
& \sin (\overrightarrow {AB} ,\,\overrightarrow {AC} ) + \cos (\overrightarrow {BC} ,\,\overrightarrow {BA} ) + \cos (\overrightarrow {CA} ,\,\overrightarrow {BA} ) \cr&= \sin {90^0} + \cos {30^0} + \cos {90^0} \cr
&= 1 + {{\sqrt 3 } \over 2} + 0 = {{2 + \sqrt 3 } \over 2} \cr} \)
Bài 7 trang 52 SGK Hình học 10 nâng cao
Cho bốn điểm bất kì \(A, B, C, D\). Chứng minh rằng:
\(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0\).
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.
Lời giải chi tiết

Ta có
\(\eqalign{
& \,\,\,\,\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \cr
& = \overrightarrow {DA} (\overrightarrow {DC} - \overrightarrow {DB} ) + \overrightarrow {DB} (\overrightarrow {DA} - \overrightarrow {DC} ) + \overrightarrow {DC} (\overrightarrow {DB} - \overrightarrow {DA} ) \cr
& = \overrightarrow {DA} \overrightarrow {DC} - \overrightarrow {DA} \overrightarrow {DB} + \overrightarrow {DB} \overrightarrow {DA} - \overrightarrow {DB} \overrightarrow {DC} + \overrightarrow {DC} \overrightarrow {DB} - \overrightarrow {DC} \overrightarrow {DA} = 0 \cr} \)
Gọi \(D\) là giao điểm của hai đường cao \(AA', BB'\) của tam giác \(ABC\).
Ta có \(\overrightarrow {DA} .\overrightarrow {BC} = 0\,;\,\,\overrightarrow {DB} .\overrightarrow {CA} = 0\)
Mà \(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0\)
Từ đó suy ra \(\overrightarrow {DC} .\overrightarrow {AB} = 0\), do đó \(DC \bot AB\).
Vậy \(D\) nằm trên đường cao \(CC'\) của tam giác \(ABC\), tức là ba đường cao trong tam giác đồng quy.
Cách khác:
Ta có thể chứng minh đẳng thức tích vô hướng bằng cách khác như sau:

Bài 8 trang 52 SGK Hình học 10 nâng cao
Chứng minh rằng điều kiện cần và đủ để tam giác \(ABC\) vuông tại \(A\) là \(\overrightarrow {BA} .\,\overrightarrow {BC} = A{B^2}\).
Lời giải chi tiết
Ta có \(\overrightarrow {BA} .\,\overrightarrow {BC} = {\overrightarrow {BA} ^2}\,\)\( \Leftrightarrow \,\,\overrightarrow {BA} (\overrightarrow {BC} - \overrightarrow {BA} ) = 0\)
\( \Leftrightarrow \overrightarrow {BA} .\,\overrightarrow {AC} = 0\,\, \Leftrightarrow \,\,BA \bot AC\)
\( \Leftrightarrow \) Tam giác \(ABC\) vuông tại \(A\).
Cách khác:
Trong tam giác ABC ta có:
\(\begin{array}{l}\overrightarrow {BA} .\overrightarrow {BC} = \overrightarrow {BA} .\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\\ = {\overrightarrow {BA} ^2} + \overrightarrow {BA} .\overrightarrow {AC} \end{array}\)
Do đó, tam giác ABC vuông tại A\( \Leftrightarrow \overrightarrow {BA} .\overrightarrow {AC} = 0\)
\( \Rightarrow \overrightarrow {BA} .\overrightarrow {BC} = {\overrightarrow {BA} ^2} + 0 = {\overrightarrow {BA} ^2}\)
Bài 9 trang 52 SGK Hình học 10 nâng cao
Cho tam giác \(ABC\) với ba đường trung tuyến \(AD, BE, CF\). Chứng minh rằng
\(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} = 0\).
Lời giải chi tiết

Vì D là trung điểm của BC nên \(\overrightarrow {AD} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
Tương tự vì E, F là trung điểm của AC, AB nên:
\(\eqalign{
& \overrightarrow {BE} = {1 \over 2}(\overrightarrow {BA} + \overrightarrow {BC} ) \cr
& \overrightarrow {CF} = {1 \over 2}(\overrightarrow {CA} + \overrightarrow {CB} ) \cr} \)
Do đó \(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} \)
\(\eqalign{
& = {1 \over 2}\overrightarrow {BC} (\overrightarrow {AB} + \overrightarrow {AC} ) + {1 \over 2}\overrightarrow {CA} (\overrightarrow {BA} + \overrightarrow {BC} ) \cr&+ {1 \over 2}\overrightarrow {AB} (\overrightarrow {CA} + \overrightarrow {CB} ) \cr
& = {1 \over 2}(\overrightarrow {BC} \overrightarrow {AB} + \overrightarrow {BC} \overrightarrow {AC} + \overrightarrow {CA} \overrightarrow {BA} \cr&+ \overrightarrow {CA} \overrightarrow {BC} + \overrightarrow {AB} \overrightarrow {CA} + \overrightarrow {AB} \overrightarrow {CB} )\cr
& = {1 \over 2}(\overrightarrow {BC} \overrightarrow {AB} + \overrightarrow {AB} \overrightarrow {CB} ) \cr&+ {1 \over 2}(\overrightarrow {BC} \overrightarrow {AC} + \overrightarrow {CA} \overrightarrow {BC} ) \cr&+ {1 \over 2}(\overrightarrow {CA} \overrightarrow {BA} + \overrightarrow {AB} \overrightarrow {CA} )\cr} \)
\(\begin{array}{l}
= \frac{1}{2}\overrightarrow {AB} \left( {\overrightarrow {BC} + \overrightarrow {CB} } \right)\\
+ \frac{1}{2}\overrightarrow {BC} \left( {\overrightarrow {AC} + \overrightarrow {CA} } \right)\\
+ \frac{1}{2}\overrightarrow {CA} \left( {\overrightarrow {BA} + \overrightarrow {AB} } \right)\\
= \frac{1}{2}\overrightarrow {AB} .\overrightarrow {BB} + \frac{1}{2}\overrightarrow {BC} .\overrightarrow {AA} + \frac{1}{2}\overrightarrow {CA} .\overrightarrow {BB} \\
= 0 + 0 + 0\\
= 0
\end{array}\)
(điều phải chứng minh)
Bài 10 trang 52 SGK Hình học 10 nâng cao
Cho hai điểm \(M, N\) nằm trên đường tròn đường kính \(AB = 2R\). Gọi \(I\) là giao điểm của hai đường thẳng \(AM, BN\).
LG a
Chứng minh rằng \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI} \,\,;\,\,\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI}.\)
Phương pháp giải:
Sửa dụng quy tắc ba điểm, xen điểm thích hợp và chú ý: \[\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\]
Lời giải chi tiết:
AB là đường kính nên \(\widehat {AMB} = \widehat {ANB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \left\{ \begin{array}{l}
AM \bot MB\\
AN \bot NB
\end{array} \right.\)
Ta có: \({\overrightarrow {AI} .\overrightarrow {AM} } = \overrightarrow {AI} \left( {\overrightarrow {AB} + \overrightarrow {BM} } \right) \)
\(= \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {AI} .\overrightarrow {BM} \)
Mặt khác: \(\overrightarrow {AI} \bot \overrightarrow {BM} \) (do AM\(\bot\) MB) nên \(\overrightarrow {AI} .\overrightarrow {BM} = 0\)
Từ đó: \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB} +0\) \(= \overrightarrow {AI} .\overrightarrow {AB}\)
Hay \(\overrightarrow {AM} .\overrightarrow {AI} = \overrightarrow {AB} .\overrightarrow {AI}\)
Ta có: \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} \left( {\overrightarrow {BA} + \overrightarrow {AN} } \right) \)\(= \overrightarrow {BI} .\overrightarrow {BA} + \overrightarrow {BI} .\overrightarrow {AN} \)
Mặt khác: \(\overrightarrow {BI} \bot \overrightarrow {AN} \) (vì BN \(\bot\) NA) nên \(\overrightarrow {BI} .\overrightarrow {AN} = 0\)
Từ đó: \(\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {BI} .\overrightarrow {BA} +0\)\(=\overrightarrow {BI} .\overrightarrow {BA}\).
Hay \(\overrightarrow {BN} .\overrightarrow {BI} = \overrightarrow {BA} .\overrightarrow {BI}.\)
LG b
Tính \(\overrightarrow {AM} .\overrightarrow {AI} + \,\,\overrightarrow {BN} .\overrightarrow {BI} \) theo \(R\).
Lời giải chi tiết:
\(\eqalign{& \overrightarrow {AM} .\overrightarrow {AI} + \overrightarrow {BN} .\overrightarrow {BI}\cr& = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} \cr & = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\cr & = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {BI} .\overrightarrow {AB} \cr&= \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) \cr & = \overrightarrow {AB} .\left( {\overrightarrow {AI} + \overrightarrow {IB} } \right)\cr &= \overrightarrow {AB} .\overrightarrow {AB} = {\overrightarrow {AB} ^2} = 4{{\rm{R}}^2} \cr} \)
Bài 11 trang 52 SGK Hình học 10 nâng cao
Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(M\). Trên \(a\) có hai điểm \(A\) và \(B\), trên \(b\) có hai điểm \(C\) và \(D\) đều khác \(M\) sao cho \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {MD} \,\,\). Chứng minh rằng bốn điểm \(A, B, C, D\) cùng nằm trên một đường tròn.
Lời giải chi tiết

Gọi \((O)\) là đường tròn ngoại tiếp tam giác \(ABC\).
Gọi \(D'\) là giao điểm của \(b\) với \((O)\) ( \({D'} \ne C\)).

Theo giả thiết ta có \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {M{D}}\)
\(\eqalign{
& \Rightarrow \,\,\overrightarrow {MC} .\overrightarrow {MD} = \overrightarrow {MC} .\overrightarrow {M{D'}} \cr
& \Rightarrow \,\,\overrightarrow {MC} (\overrightarrow {MD} - \overrightarrow {M{D'}} ) = 0 \cr
& \Rightarrow \,\,\overrightarrow {MC} .\,\overrightarrow {{D'}D} = 0\,\,\,\, \cr} \)
\(\Rightarrow \,\overrightarrow {{D'}D} = 0\) (Do \(M, C, D, D'\) cùng thuộc đường thẳng b nên \(\overrightarrow {MC} \) và \(\overrightarrow {{D'}D}\) không thể vuông góc với nhau)
\( \Rightarrow D \equiv {D'}\).
Vậy bốn điểm \(A, B, C, D\) cùng nằm trên một đường tròn.
Bài 12 trang 52 SGK Hình học 10 nâng cao
Cho đoạn thẳng \(AB\) cố định, \(AB = 2a\) và một số \({k^2}\). Tìm tập hợp các điểm \(M\) sao cho \(M{A^2} - M{B^2} = {k^2}\)
Lời giải chi tiết

Gọi \(O\) là trung điểm đoạn \(AB, H\) là hình chiếu của \(M\) lên \(AB\). Ta có
\(\eqalign{
& M{A^2} - M{B^2} = {k^2}\cr& \Leftrightarrow \,\,{\overrightarrow {MA} ^2} - {\overrightarrow {MB} ^2} = {k^2} \cr
& \Leftrightarrow (\overrightarrow {MA} + \overrightarrow {MB} ).\,(\overrightarrow {MA} - \overrightarrow {MB} ) = {k^2} \cr
& \Leftrightarrow 2\overrightarrow {MO} .\,\overrightarrow {BA} = {k^2}\, \cr
& \Leftrightarrow 2\left( {\overrightarrow {MH} + \overrightarrow {HO} } \right).\overrightarrow {BA}=k^2 \cr
& \Leftrightarrow 2\overrightarrow {MH} .\overrightarrow {BA} + 2\overrightarrow {HO} .\overrightarrow {BA} = {k^2}\cr&\Leftrightarrow 2\overrightarrow {HO} .\,\overrightarrow {BA} = {k^2} \cr} \)
(Vì \(\overrightarrow {MH} .\overrightarrow {BA} = \overrightarrow 0 \))
\(\begin{array}{l}
\Leftrightarrow 2HO.BA\cos \left( {\overrightarrow {HO} ,\overrightarrow {BA} } \right) = {k^2}\\
\Leftrightarrow 2HO.BA.\cos {0^0} = {k^2}\\
\Leftrightarrow 2HO.BA = {k^2}\\
\Leftrightarrow HO = \frac{{{k^2}}}{{2BA}} = \frac{{{k^2}}}{{2.2a}} = \frac{{{k^2}}}{{4a}}
\end{array}\)
Suy ra \(H\) cố định nằm trên tia \(OB\) và \(OH = {{{k^2}} \over {4a}}\).
Do \(H\) là hình chiếu của \(M\) lên \(AB\) nên tập hợp các điểm \(M\) là đường thẳng vuông góc với \(AB\) tại \(H, H\) nằm trên tia \(OB\) sao cho \(OH = {{{k^2}} \over {4a}}\).
Bài 13 trang 52 SGK Hình học 10 nâng cao
Trong mặt phẳng tọa độ, cho \(\overrightarrow u = {1 \over 2}\overrightarrow i - 5\overrightarrow j \) và \(\overrightarrow v = k\overrightarrow i - 4\overrightarrow j \).
LG a
Tìm các giá trị của \(k\) để \(\overrightarrow u \bot \overrightarrow v \)
Phương pháp giải:
Sủ dụng lí thuyết: \(\overrightarrow u \bot \overrightarrow v \,\, \Leftrightarrow \,\,\overrightarrow u .\,\overrightarrow v = 0\,\)
Lời giải chi tiết:
Ta có \(\overrightarrow u = ({1 \over 2}\,;\, - 5)\,;\overrightarrow v = (k\,;\, - 4)\,\).
\(\overrightarrow u \bot \overrightarrow v \,\, \Leftrightarrow \,\,\overrightarrow u .\,\overrightarrow v = 0\,\)
\(\Leftrightarrow \,\,{1 \over 2}.k + ( - 5).( - 4) = 0\)
\( \Leftrightarrow \frac{k}{2} + 20 = 0 \Leftrightarrow \frac{k}{2} = - 20\)\(\Leftrightarrow \,\,k = - 40.\)
LG b
Tìm các giá trị của \(k\) để \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow v } \right|\)
Phương pháp giải:
Tính độ dài mỗi véc tơ rồi cho chúng bằng nhau tìm k.
Chú ý: \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {{x_N} - {x_M}} \right)}^2} + {{\left( {{y_N} - {y_M}} \right)}^2}} \)
Lời giải chi tiết:
\(\begin{array}{l}
\left| {\overrightarrow u } \right| = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( { - 5} \right)}^2}} = \frac{{\sqrt {101} }}{2}\\
\left| {\overrightarrow v } \right| = \sqrt {{k^2} + {{\left( { - 4} \right)}^2}} = \sqrt {{k^2} + 16} \\
\Rightarrow \left| {\overrightarrow u } \right| = \left| {\overrightarrow v } \right| \Leftrightarrow \frac{{\sqrt {101} }}{2} = \sqrt {{k^2} + 16} \\
\Leftrightarrow \frac{{101}}{4} = {k^2} + 16\\
\Leftrightarrow {k^2} = \frac{{37}}{4}\\
\Leftrightarrow k = \pm \frac{{\sqrt {37} }}{2}
\end{array}\)
Bài 14 trang 52 SGK Hình học 10 nâng cao
Trong mặt phẳng tọa độ, cho tam giác \(ABC\) có các đỉnh \(A( - 4\,;\,1),\,B(2\,;\,4),\,C(2\,;\, - 2)\)
LG a
Tính chu vi và diện tích của tam giác đó.
Lời giải chi tiết:

Ta có \(\overrightarrow {AB} = (6\,;\,3)\,,\overrightarrow {AC} = (6\,;\, - 3),\) \(\overrightarrow {BC} = (0\,;\, - 6).\)
Suy ra
\(\eqalign{
& AB = \sqrt {{6^2} + {3^2}} = \sqrt {45} = 3\sqrt 5 \cr
& AC = \sqrt {{6^2} + {{( - 3)}^2}} = \sqrt {45} = 3\sqrt 5 \cr
& BC = \sqrt {{0^2} + {{( - 6)}^2}} = \sqrt {36} = 6 \cr} \)
Tam giác \(ABC\) cân tại \(A\).
Chu vi tam giác \(ABC\) là \(3\sqrt 5 + 3\sqrt 5 + 6 = 6\sqrt 5 + 6\).
Gọi \(M\) là trung điểm của \(BC\) thì \(AM\) là đường cao của ta giác \(ABC\).
Ta có \(M(2\,;\,1)\,,\,\,\overrightarrow {AM} = (6\,;\,0)\) \(\Rightarrow AM = \sqrt {{6^2} + 0} = 6\).
Diện tích tam giác \(ABC\) là
\({S_{ABC}} = {1 \over 2}BC.AM = {1 \over 2}.6.6 = 18\)
LG b
Tìm tọa độ của trọng tâm \(G\), trực tâm \(H\) và tâm \(I\) của đường tròn ngoại tiếp tam giác \(ABC\). Từ đó hãy kiểm tra tính chất thẳng hàng của ba điểm \(I, G, H\).
Lời giải chi tiết:
Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là
\(\left\{ \matrix{
{x_G} = {1 \over 3}({x_A} + {x_B} + {x_C}) = {1 \over 3}( - 4 + 2 + 2) = 0 \hfill \cr
{y_G} = {1 \over 3}({y_A} + {y_B} + {y_C}) = {1 \over 3}(1 + 4 - 2) = 1 \hfill \cr} \right.\,\)
Vậy \(G\,(0\,;\,1)\).
Gọi \(H\,({x_H}\,,\,{y_H})\) là trực tâm tam giác \(ABC\) \( \Rightarrow AH \bot BC\) và \(BH \bot AC\)
Ta có
\(\eqalign{
& \left\{ \matrix{
\overrightarrow {AH} .\,\overrightarrow {BC} = 0 \hfill \cr
\overrightarrow {BH} .\,\overrightarrow {AC} = 0 \hfill \cr} \right.\cr& \Leftrightarrow \,\,\left\{ \matrix{
({x_H} + 4).0 + ({y_H} - 1).( - 6) = 0 \hfill \cr
({x_H} - 2).6 + ({y_H} - 4).( - 3) = 0 \hfill \cr} \right.\,\, \cr
& \Leftrightarrow \,\,\left\{ \matrix{
{x_H} = {1 \over 2}\hfill \cr
{y_H} = 1 \hfill \cr} \right. \cr} \)
Vậy \(H\,\left( {{1 \over 2}\,;\,1} \right)\).
Gọi \(I\,({x_I}\,,\,{y_I})\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Ta có
\(\eqalign{
& \left\{ \matrix{
A{I^2} = B{I^2} \hfill \cr
A{I^2} = C{I^2} \hfill \cr} \right.\cr& \Leftrightarrow \,\,\left\{ \matrix{
{({x_I} + 4)^2} + {({y_I} - 1)^2} = {({x_I} - 2)^2} + {({y_I} - 4)^2} \hfill \cr
{({x_I} + 4)^2} + {({y_I} - 1)^2} = {({x_I} - 2)^2} + {({y_I} + 2)^2} \hfill \cr} \right. \cr
& \Leftrightarrow \,\,\left\{ \matrix{
{x_I}^2 + 8{x_I} + 16 + {y_I}^2 - 2{y_I} + 1 = {x_I}^2 - 4{x_I} + 4 + {y_I}^2 - 8{y_I} + 16 \hfill \cr
{x_I}^2 + 8{x_I} + 16 + {y_I}^2 - 2{y_I} + 1 = {x_I}^2 - 4{x_I} + 4 + {y_I}^2 + 4{y_I} + 4 \hfill \cr} \right. \cr
& \Leftrightarrow \,\,\left\{ \matrix{
4{x_I} + 2{y_I} = 1 \hfill \cr
4{x_I} - 2{y_I} = - 3 \hfill \cr} \right.\cr& \Leftrightarrow \,\,\left\{ \matrix{
{x_I} = - {1 \over 4} \hfill \cr
{y_I} = 1 \hfill \cr} \right. \cr} \)
Vậy \(I\,( - {1 \over 4}\,;\,1)\).
Khi đó, ta có \(\overrightarrow {IG} = \left( {{1 \over 4}\,;\,0} \right)\,,\,\,\,\overrightarrow {IH} = \left( {{3 \over 4}\,;\,0} \right)\).
Do đó \(\overrightarrow {IG} = {1 \over 3}\overrightarrow {IH} \)
Suy ra \(I, G, H\) thẳng hàng.
Được cập nhật: 18 tháng 4 lúc 8:41:16 | Lượt xem: 398




