Câu 1 trang 109 SGK Đại số 10 nâng cao
Chứng minh rằng, nếu \(a > b\) và \(ab > 0\); \({1 \over a} < {1 \over b}\)
Phương pháp giải - Xem chi tiết
Biến đổi tương đương bất phương trình đưa về 1 bđt đúng.
Lời giải chi tiết
Ta có:
\({1 \over a} < {1 \over b} \Leftrightarrow {1 \over b} - {1 \over a} > 0 \Leftrightarrow {{a - b} \over {ab}} > 0\)
(đúng vì a > b nên \(a – b > 0\) và \(ab > 0\))
Vậy \({1 \over a} < {1 \over b}\)
Câu 2 trang 109 SGK Đại số 10 nâng cao
Chứng minh rằng nửa chu vi của tam giác lớn hơn mỗi cạnh của tam giác đó.
Lời giải chi tiết
Gọi a, b, c là ba cạnh của một tam giác
Nửa chu vi của tam giác đó là \(p = {{a + b + c} \over 2}\)
Ta có:
\(p - a = {{a + b + c - 2a} \over 2} = {{b + c - a} \over 2}\)
Vì \(b + c > a\) nên \({{b + c - a} \over 2}>0\) hay \(p > a\)
Chứng minh tương tự, ta có: \(p > b\) và \(p > c\)
Cách khác:
Ta chứng minh: p > a.
Các bất đẳng thức p> b và p> c thì chứng minh tương tự.
Thật vậy, theo bất đẳng thức tam giác: tổng độ dài hai cạnh luôn lớn hơn độ dài cạnh còn lại nên ta có:
b + c > a ⇔ a+ b+ c > 2a \( \Rightarrow \frac{{a + b + c}}{2} > a \Rightarrow dpcm\)
Câu 3 trang 109 SGK Đại số 10 nâng cao
Chứng minh rằng a2 + b2 + c2 ≥ ab + bc + ca với mọi số thực a, b, c.
Đẳng thức xảy ra khi và chỉ khi a = b = c.
Lời giải chi tiết
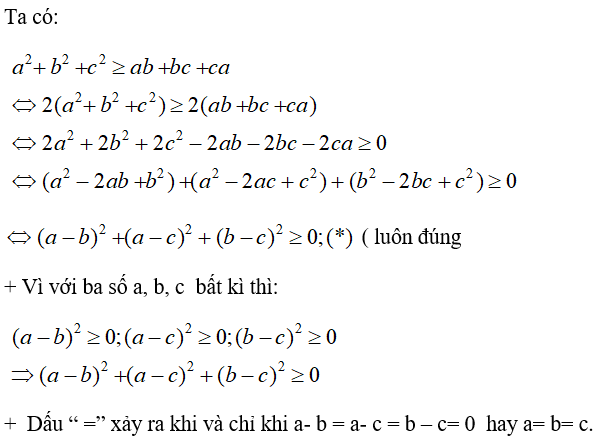
Câu 4 trang 109 SGK Đại số 10 nâng cao
Hãy so sánh các kết quả sau đây:
LG a
\(\sqrt {2000} + \sqrt {2005} \) và \(\sqrt {2002} + \sqrt {2003} \) (không dùng bảng số hoặc máy tính)
Lời giải chi tiết:
Giả sử: \(\sqrt {2000} + \sqrt {2005} \, < \sqrt {2002} + \sqrt {2003} \,\,\,\,\,(1)\)
Ta có:
\(\eqalign{
& (1)\cr & \Leftrightarrow \,{(\sqrt {2000} + \sqrt {2005} )^2}\, < {(\sqrt {2002} + \sqrt {2003} \,)^2} \cr
& \Leftrightarrow 2000 + 2\sqrt {2000.2005} + 2005 \cr &< 2002 + 2\sqrt {2002.2003} + 2003\cr &\Leftrightarrow 4005 + 2\sqrt {2000.2005} < 4005 + 2\sqrt {2002.2003} \cr
& \Leftrightarrow 2000.2005 < 2002.2003 \cr
& \Leftrightarrow 2000.2005 < (2000 + 2)(2005 - 2) \cr
& \Leftrightarrow 2000.2005 < 2000.2005 + 6 \cr} \)
Ta thấy kết quả suy ra luôn đúng.
Do đó: \(\sqrt {2000} + \sqrt {2005} < \sqrt {2002} + \sqrt {2003} \)
LG b
\(\sqrt {a + 2} + \sqrt {a + 4} \) và \(\sqrt a + \sqrt {a + 6} \,\,(a \ge 0)\)
Lời giải chi tiết:
Giả sử:
\(\sqrt {a + 2} + \sqrt {a + 4} ≤ \sqrt a + \sqrt {a + 6} \,\,(a \ge 0)\) (2)
Ta có:
\(\eqalign{
& (2) \Leftrightarrow {(\sqrt {a + 2} + \sqrt {a + 4} )^2} \le {(\sqrt a + \sqrt {a + 6} )^2} \cr
& \Leftrightarrow a + 2 + 2\sqrt {\left( {a + 2} \right)\left( {a + 4} \right)} + a + 4 \cr &\le a + 2\sqrt {a\left( {a + 6} \right)} + a + 6\cr &\Leftrightarrow 2a + 6 + 2\sqrt {(a + 2)(a + 4)}\cr& \le 2a + 6 + 2\sqrt {a(a + 6)} \cr
& \Leftrightarrow (a + 2)(a + 4) \le a(a + 6) \cr
& \Leftrightarrow {a^2} + 6a + 8 \le {a^2} + 6a \cr
& \Leftrightarrow 8 \le 0 \cr} \)
Ta thấy : \(8 ≤ 0\) là vô lý
Vậy \(\sqrt {a + 2} + \sqrt {a + 4} > \sqrt a + \sqrt {a + 6} \,\,(a \ge 0)\)
Câu 5 trang 110 SGK Đại số 10 nâng cao
Chứng minh rằng, nếu a > 0 và b > 0 thì \({1 \over a} + {1 \over b} \ge {4 \over {a + b}}\)
Phương pháp giải
Biến đổi tương đường đưa về một bđt luôn đúng suy ra đpcm.
Lời giải chi tiết
Với \(a > 0, b > 0\), ta có:
\(\eqalign{
& {1 \over a} + {1 \over b} \ge {4 \over {a + b}} \cr &\Leftrightarrow {{a + b} \over {ab}} \ge {4 \over {a + b}} \cr&\Leftrightarrow {(a + b)^2} \ge 4ab \cr
& \Leftrightarrow {a^2} + 2ab + {b^2} \ge 4ab \cr &\Leftrightarrow {a^2} - 2ab + {b^2} \ge 0\cr &\Leftrightarrow {(a - b)^2} \ge 0 \cr} \)
Ta thấy điều này luôn đúng
Vậy \({1 \over a} + {1 \over b} \ge {4 \over {a + b}}\)
Đẳng thức xảy ra khi \(a = b\).
Cách khác:
Áp dụng bđt Cô si ta có:
\(\begin{array}{l}
\frac{1}{a} + \frac{1}{b} \ge 2\sqrt {\frac{1}{a}.\frac{1}{b}} = \frac{2}{{\sqrt {ab} }}\\
a + b \ge 2\sqrt {ab} \\
\Rightarrow \left( {\frac{1}{a} + \frac{1}{b}} \right)\left( {a + b} \right)\\
\ge \frac{2}{{\sqrt {ab} }}.2\sqrt {ab} = 4\\
\Rightarrow \left( {\frac{1}{a} + \frac{1}{b}} \right)\left( {a + b} \right) \ge 4\\
\Rightarrow \frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}
\end{array}\)
Câu 6 trang 110 SGK Đại số 10 nâng cao
Chứng minh rằng nếu a ≥ 0 và b ≥ 0 thì a3 + b3 ≥ ab(a + b). Khi nào đẳng thức xảy ra?
Lời giải chi tiết
Ta có a3 + b3 ≥ ab(a + b)
⇔ (a+ b).(a2 – ab + b2 ) – ab (a+ b) ≥ 0
⇔ (a + b)(a2 - ab + b2 – ab) ≥ 0
⇔ (a + b)(a2 - 2ab + b2) ≥ 0
⇔ (a + b)(a - b)2 ≥ 0 (*)
Bất đẳng thức (*) luôn đúng vì với a ≥ 0; b ≥ 0 thì a+b ≥ 0 và (a- b)2 ≥ 0
=> Bất đẳng thức a3 + b3 ≥ ab(a + b) luôn đúng với a ≥ 0; b ≥ 0
*Dấu “=” xảy ra khi và chỉ khi:
\(\left[ \begin{array}{l}a + b = 0\\{\left( {a - b} \right)^2} = 0\end{array} \right. \Leftrightarrow a = b\)
Câu 7 trang 110 SGK Đại số 10 nâng cao
LG a
Chứng minh rằng a2 + ab + b2 ≥ 0 với mọi số thực a, b.
Phương pháp giải:
Biến đổi về hằng đẳng thức bậc hai.
Lời giải chi tiết:
Ta có:
\(\eqalign{
& {a^2} + ab + {b^2} \ge 0\cr & \Leftrightarrow {a^2} + 2a{b \over 2} + {{{b^2}} \over 4} + {{3{b^2}} \over 4} \ge 0 \cr
& \Leftrightarrow {(a + {b \over 2})^2} + {{3{b^2}} \over 4} \ge 0 \cr} \)
Ta thấy điều trên luôn đúng nên suy ra đpcm.
Dấu = xảy ra khi
\(\left\{ \begin{array}{l}
{\left( {a + \frac{b}{2}} \right)^2} = 0\\
\frac{{3{b^2}}}{4} = 0
\end{array} \right. \Leftrightarrow a = b = 0\)
LG b
Chứng minh rằng với mọi số thực a, b tùy ý, ta có a4 + b4 ≥ a3b + ab3
Phương pháp giải:
Biến đổi tương đương, chuyển vế đưa về bất đẳng thức luôn đúng.
Lời giải chi tiết:
Ta có:
\(\eqalign{
& {a^4} + {b^4} \ge {\rm{ }}{a^3}b + a{b^3} \cr&\Leftrightarrow {a^4} - {a^3}b - a{b^3} + {b^4} \ge 0 \cr
& \Leftrightarrow {a^3}(a - b) - {b^3}(a - b) \ge 0 \cr
& \Leftrightarrow (a - b)({a^3} - {b^3}) \ge 0 \cr
& \Leftrightarrow {(a - b)^2}({a^2} + ab + {b^2}) \ge 0 \cr} \)
Ta thấy rằng điều này luôn đúng vì \({\left( {a - b} \right)^2} \ge 0,{a^2} + ab + {b^2} \ge 0,\forall a,b\)
Vậy a4 + b4 ≥ a3b + ab3 với mọi a, b.
Dấu "=" xảy ra khi a=b.
Câu 8 trang 110 SGK Đại số 10 nâng cao
Chứng minh rằng nếu a, b và c là độ dài ba cạnh một tam giác thì a2 + b2 + c2 < 2(ab + bc + ca).
Phương pháp giải
Sử dụng bđt tam giác: Tổng hai cạnh luôn lớn hơn cạnh thứ ba.
Kết hợp tính chất nhân cả hai vế của bđt với một số dương thì bđt không đổi chiều.
Lời giải chi tiết
Do a, b, c là ba cạnh của tam giác nên
\(\eqalign{
& a < b + c \Rightarrow {a^2} < a\left( {b + c} \right) \cr &\Rightarrow {a^2} < ab + ac\,\,\,(1) \cr
& b < a + c \Rightarrow {b^2} < b(a+c) \cr &\Rightarrow {b^2} <ba + bc\,\,(2) \cr
& c < a + b \Rightarrow {c^2} < c(a+b)\cr & \Rightarrow {c^2} < ca + cb\,\,\,(3)\cr} \)
Cộng vế với vế của ba bất đẳng thức (1), (2), (3) ta được: \({a^2} + {b^2} + {c^2} < ab + ac + ba + bc + ca + cb\) \(\Rightarrow {a^2} + {b^2} + {c^2} < 2\left( {ab + bc + ca} \right)\)
Câu 9 trang 110 SGK Đại số 10 nâng cao
Chứng minh rằng nếu a ≥ 0 và b ≥ 0 thì: \({{a + b} \over 2}.{{{a^2} + {b^2}} \over 2} \le {{{a^3} + {b^3}} \over 2}\)
Phương pháp giải
Biến đổi tương đương đưa về các bđt luôn đúng.
Lời giải chi tiết
Ta có:
\(\eqalign{
& {{a + b} \over 2}.{{{a^2} + {b^2}} \over 2} \le {{{a^3} + {b^3}} \over 2}\cr& \Leftrightarrow \left( {a + b} \right)\left( {{a^2} + {b^2}} \right) \le 2\left( {{a^3} + {b^3}} \right)\cr & \Leftrightarrow {a^3} + a{b^2} + {a^2}b + {b^3} \le 2{a^3} + 2{b^3} \cr
& \Leftrightarrow {a^3} - a{b^2} - {a^2}b + {b^3} \ge 0 \cr
& \Leftrightarrow a\left( {{a^2} - {b^2}} \right) - b\left( {{a^2} - {b^2}} \right) \ge 0\cr &\Leftrightarrow (a - b)({a^2} - {b^2}) \ge 0 \cr
& \Leftrightarrow {(a - b)^2}(a + b) \ge 0 \cr} \)
Điều suy ra luôn đúng do với a ≥ 0; b ≥ 0 thì (a - b)2 ≥ 0, a + b ≥ 0.
Vậy \({{a + b} \over 2}.{{{a^2} + {b^2}} \over 2} \le {{{a^3} + {b^3}} \over 2}\).
Dấu "=" xảy ra khi
\(\left[ \begin{array}{l}
{\left( {a - b} \right)^2} = 0\\
a + b = 0
\end{array} \right. \Leftrightarrow a = b\)
Câu 10 trang 110 SGK Đại số 10 nâng cao
LG a
Chứng minh rằng, nếu \(x ≥ y ≥ 0\) thì \({x \over {1 + x}} \ge {y \over {1 + y}}\)
Phương pháp giải:
Biến đổi tương đương về các bđt luôn đúng.
Lời giải chi tiết:
Với \(x ≥ y ≥ 0\) , ta có:
\(\eqalign{
& {x \over {1 + x}} \ge {y \over {1 + y}} \cr &\Leftrightarrow x(1 + y) \ge y(1 + x) \cr
& \Leftrightarrow x + xy \ge y + xy \Leftrightarrow x \ge y \cr} \)
Điều này đúng với giả thiết.
Vậy ta được điều cần phải chứng minh.
Dấu = xảy ra khi x=y.
LG b
Chứng minh rằng đối với hai số tùy ý a, b ta có: \({{|a - b|} \over {1 + |a - b|}} \le {{|a|} \over {1 + |a|}} + {b \over {1 + |b|}}\)
Phương pháp giải:
Áp dụng bất đẳng thức ý a với x=|a|+|b|; y=|a - b|
Lời giải chi tiết:
Vì \(|a| + |b|≥ |a – b| \) nên theo câu a ta có:
\({{|a - b|} \over {1 + |a - b|}} \le {{|a| + |b|} \over {1 + |a| + |b|}} \) \(= {{|a|} \over {1 + |a| + |b|}} + {{|b|} \over {1 + |a| + |b|}} \)
\(\le {{|a|} \over {1 + |a|}} + {{|b|} \over {1 + |b|}}\)
Dấu “=” xảy ra khi có ít nhất một số bằng 0 ( tức là a = 0 hoặc b = 0 hoặc a = b = 0).
Câu 11 trang 110 SGK Đại số 10 nâng cao
Chứng minh rằng:
LG a
Nếu a, b là hai số cùng dấu thì \({a \over b} + {b \over a} \ge 2\)
Phương pháp giải:
Áp dụng bđt Cô si cho hai số dương \(a + b \ge 2\sqrt {ab} \)
Lời giải chi tiết:
Nếu a, b là hai số cùng dấu thì \({a \over b}\,;\,{b \over a}\) là hai số dương nên:
\({a \over b} + {b \over a} \ge 2\sqrt {{a \over b}.{b \over a}} = 2\) (theo bất đẳng thức Cô-si)
Dấu = xảy ra khi \(\frac{a}{b} = \frac{b}{a} \Leftrightarrow a = b\) (do a,b cùng dấu).
LG b
Nếu a, b là hai số trái dấu thì \({a \over b} + {b \over a} \le - 2\)
Lời giải chi tiết:
Nếu a, b là hai số trái dấu thì \(\dfrac{a}{b} < 0,\dfrac{b}{a} < 0\) \( \Rightarrow - \dfrac{a}{b} > 0, - \dfrac{b}{a} > 0\)
Áp dụng bđt Cô si cho hai số dương \(- \dfrac{a}{b} > 0, - \dfrac{b}{a}\) ta có:
\(\left( { - \dfrac{a}{b}} \right) + \left( { - \dfrac{b}{a}} \right)\) \( \ge 2\sqrt {\left( { - \dfrac{a}{b}} \right).\left( { - \dfrac{b}{a}} \right)} = 2 \) \(\Rightarrow - \left( {\dfrac{a}{b} + \dfrac{b}{a}} \right) \ge 2\) \( \Rightarrow \dfrac{a}{b} + \dfrac{b}{a} \le - 2\)
Dấu = xảy ra khi \( - \dfrac{a}{b} = - \dfrac{b}{a} \Leftrightarrow {a^2} = {b^2} \Leftrightarrow a = - b\) do a,b trái dấu.
Câu 12 trang 110 SGK Đại số 10 nâng cao
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f(x) = (x + 3)(5 – x)\) với \(-3 ≤ x ≤ 5\)
Phương pháp giải
- Sử dụng bđt Cô si cho hai số dương x+3 và 5-x tìm GTLN.
- Đánh giá GTNN của tích dựa vào điều kiện \(-3 ≤ x ≤ 5\).
Lời giải chi tiết
Vì -3 ≤ x ≤ 5 nên x + 3 ≥ 0; 5 - x ≥ 0
* Áp dụng bất đẳng thức Cô- si cho hai số không âm x + 3 và 5 – x ta được:
\(\begin{array}{l}x + 3 + 5 - x \ge 2\sqrt {\left( {x + 3} \right)\left( {5 - x} \right)} \\ \Leftrightarrow 8 \ge 2\sqrt {\left( {x + 3} \right)\left( {5 - x} \right)} \\ \Leftrightarrow 4 \ge \sqrt {\left( {x + 3} \right)\left( {5 - x} \right)} \\ \Leftrightarrow 16 \ge \left( {x + 3} \right)\left( {5 - x} \right)\\ \Rightarrow \left( {x + 3} \right)\left( {5 - x} \right) \le 16\end{array}\)
Do đó, giá trị lớn nhất của (x + 3). (5 - x) là 16
Dấu “=” xảy ra khi: \(x - 3 = 5 - x \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\)
* Do x + 3 ≥ 0; 5 - x ≥ 0 nên (x + 3).(5 - x) ≥ 0
Lại thấy f(-3) = f(5) = 0
Do đó, giá trị nhỏ nhất của hàm số f(x) là 0.
Dấu “=” xảy ra khi x= -3 hoặc x= 5.
Câu 13 trang 110 SGK Đại số 10 nâng cao
Tìm giá trị nhỏ nhất của hàm số \(f(x) = x + {2 \over {x - 1}}\) với x > 1.
Phương pháp giải
Thêm bớt 1 và áp dụng bđt Cô si cho hai số dương x-1 và \({2 \over {x - 1}}\).
Lời giải chi tiết
Vì x > 1 nên x – 1 và \({2 \over {x - 1}}\) là hai số dương.
Do đó:
\(f(x) = x + {2 \over {x + 1}} = 1 + (x - 1) + {2 \over {x - 1}} \) \(\ge 1 + 2\sqrt {(x - 1){2 \over {x - 1}}} = 1 + 2\sqrt 2 \)
Dấu “=” xảy ra khi và chỉ khi \(x - 1 = {2 \over {x - 1}} \) \(\Leftrightarrow {\left( {x - 1} \right)^2} = 2 \Leftrightarrow x = 1 + \sqrt 2 \)
Vậy giá trị nhỏ nhất của f(x) là \( 1 + 2\sqrt 2 \) khi \(x = 1 + \sqrt 2 \).
Câu 14 trang 112 SGK Đại số 10 nâng cao
Chứng minh rằng nếu a, b, c là ba số dương thì: \({{{a^4}} \over b} + {{{b^4}} \over c} + {{{c^4}} \over a} \ge 3abc\)
Phương pháp giải
Áp dụng bất đẳng thức Cô-si cho ba số dương \(a + b + c \ge 3\sqrt[3]{{abc}}\)
Lời giải chi tiết
Do a,b,c> 0 nên \(\frac{{{a^4}}}{b},\frac{{{b^4}}}{c},\frac{{{c^4}}}{a} > 0\).
Áp dụng bất đẳng thức Cô-si cho ba số dương \(\frac{{{a^4}}}{b},\frac{{{b^4}}}{c},\frac{{{c^4}}}{a}\) ta có:
\({{{a^4}} \over b} + {{{b^4}} \over c} + {{{c^4}} \over a} \ge 3\root 3 \of {{{{a^4}} \over b}.{{{b^4}} \over c}.{{{c^4}} \over a}} = 3abc\)
Dấu “=”xảy ra \( \Leftrightarrow {{{a^4}} \over b} = {{{b^4}} \over c} = {{{c^4}} \over a} \Leftrightarrow a = b = c\)
Câu 15 trang 112 SGK Đại số 10 nâng cao
Một khách hàng đến một cửa hàng bán hoa quả mua 2kg cam đã yêu cầu cân hai lần. Lần đầu, người bán hàng đặt quả cân 1kg lên đĩa cân bên phải và đặt cam lên đĩa cân bên trái cho đến khi cân thăng bằng và lần sau, đặt quả cân 1kg lên đĩa cân bên trái và cam lên đĩa cân bên phải cho đến khi cân thăng bằng. Nếu cái cân đĩa đó không chính xác (do hai cánh tay đòn dài, ngắn khác nhau) nhưng quả cân là đúng 1kg thì khách hàng có mua được đúng 2kg cam hay không? Vì sao?
Lời giải chi tiết
Gọi a và b theo thứ tự là độ dài cánh tay đòn bên phải và bên trái của cái cân đĩa (a > 0; b > 0; đơn vị: cm)
Trong lần cân đầu, khối lượng cam được cân là \({a \over b}\) (kg)
Trong lần cân thứ hai, khối lượng cam được cân là \({b \over a}\) (kg)
Do đó, khối lượng cam được cân cả hai lần là \(({a \over b} + {b \over a})\,(kg)\)
Nếu cái cân đĩa đó không chính xác, tức a ≠ b, thì vì \({a \over b} + {b \over a} > 2\) nên khách hàng mua được nhiều hơn 2kg cam.
Câu 16 trang 112 SGK Đại số 10 nâng cao
Chứng minh rằng với mọi số nguyên n, ta có:
LG a
\({1 \over {1.2}} + {1 \over {2.3}} + {1 \over {3.4}} + ....\, + {1 \over {n(n + 1)}} < 1\)
Phương pháp giải:
\({1 \over {1.2}} = 1 - {1 \over 2};\,{1 \over {2.3}} = {1 \over 2} - {1 \over 3};\,....\,\,\,\)
Lời giải chi tiết:
Ta có: \({1 \over {k(k + 1)}} = {{(k + 1) - k} \over {k(k + 1)}} = {1 \over k} - {1 \over {k + 1}}\,\,\,\forall k \ge 1\)
Do đó:
\(\eqalign{
& {1 \over {1.2}} + {1 \over {2.3}} + {1 \over {3.4}} + ....\, + {1 \over {n(n + 1)}} \cr&= 1 - {1 \over 2} + {1 \over 2} - {1 \over 3} + ... + {1 \over n} - {1 \over {n + 1}} \cr
& = 1 - {1 \over {n + 1}} < 1 \cr} \)
LG b
\({1 \over {{1^2}}} + {1 \over {{2^2}}} + {1 \over {{3^2}}} + ....+ {1 \over {{n^2}}} < 2\)
Lời giải chi tiết:
Ta có: \({1 \over {{k^2}}} < {1 \over {k(k - 1)}} \Rightarrow {1 \over {{k^2}}} < {1 \over {k - 1}} - {1 \over k}\,\,\,(k \le 2)\)
Do đó:
\(\begin{array}{l}
\frac{1}{{{1^2}}} + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{n^2}}}\\
< 1 + \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{\left( {n - 1} \right).n}}\\
= 1 + 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{n - 1}} - \frac{1}{n}\\
= 2 - \frac{1}{n} < 2
\end{array}\)
Câu 17 trang 112 SGK Đại số 10 nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
\(A = \sqrt {x - 1} + \sqrt {4 - x} \)
Phương pháp giải
Bình phương biểu thức A, từ đó đánh giá GTLN dựa vào bđt Cô si \(2\sqrt {ab} \le a + b\) và GTNN dựa vào tính chất căn bậc hai \(\sqrt P \ge 0\).
Lời giải chi tiết
Điều kiện: \(1 ≤ x ≤ 4\)
Với \(1 ≤ x ≤ 4\), ta có:
\({A^2} = {(\sqrt {x - 1} + \sqrt {4 - x} )^2} \)
\( = 3 + 2\sqrt {(x - 1)(4 - x)} \) \(\le 3 + x - 1 + 4 - x = 6\)
(Theo bất đẳng thức Cô-si)
Suy ra: \(A \le \sqrt 6 \)
Dấu “=” xảy ra khi \(x – 1= 4 – x \) \( \Rightarrow x = {5 \over 2}\) (thỏa mãn điều kiện : \(1 ≤ x ≤ 4\))
Vậy giá trị lớn nhất của A là \(\sqrt 6 \) đạt được khi \(x = {5 \over 2}\).
\({A^2} = 3 + 2\sqrt {(x - 1)(4 - x)} \ge 3\)
vì \(\sqrt {(x - 1)(4 - x)} \ge 0\)
Vậy \(A \ge \sqrt 3 \) đạt được khi x=1 hoặc x=4.
Câu 18 trang 112 SGK Đại số 10 nâng cao
Chứng minh rằng với mọi số thực a, b, ta có:
(a + b + c)2 ≤ 3(a2 + b2 + c2)
Phương pháp giải
Biến đổi tương đương bđt đưa về bđt luôn đúng.
Lời giải chi tiết
Ta có:
(a + b + c)2 ≤ 3(a2 + b2 + c2)
⇔ a2 + b2 + c2 +2ab + 2bc + 2ca ≤ 3a2 + 3b2 + 3c2
⇔ 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca ≥ 0
⇔ (a2 - 2ab + b2 )+ (b2 - 2bc + c2 )+ (c2 - 2ca + a2 )≥ 0
⇔ (a – b)2 + (b – c)2 + (c – a)2 ≥ 0 (luôn đúng do (a – b)2 ≥ 0, (b – c)2 ≥ 0, (c – a)2 ≥ 0).
Vậy (a + b + c)2 ≤ 3(a2 + b2 + c2).
Dấu = xảy ra khi
\(\left\{ \begin{array}{l}
{\left( {a - b} \right)^2} = 0\\
{\left( {b - c} \right)^2} = 0\\
{\left( {c - a} \right)^2} = 0
\end{array} \right. \Leftrightarrow a = b = c\)
Câu 19 trang 112 SGK Đại số 10 nâng cao
Chứng minh rằng nếu a, b, c, d là bốn số không âm thì:
\({\left({{a + b + c + d} \over 4}\right)^4} \ge abcd\)
Lời giải chi tiết
Theo bất đẳng thức Cô-si, ta có:
\(\begin{array}{l}
\frac{{a + b + c + d}}{4} = \frac{1}{2}.\frac{{a + b + c + d}}{2}\\
= \frac{1}{2}\left( {\frac{{a + b}}{2} + \frac{{c + d}}{2}} \right)\\
\ge \frac{1}{2}.\left( {\frac{{2\sqrt {ab} }}{2} + \frac{{2\sqrt {cd} }}{2}} \right)\\
= \frac{1}{2}\left( {\sqrt {ab} + \sqrt {cd} } \right)\\
\ge \frac{1}{2}.2\sqrt {\sqrt {ab} .\sqrt {cd} } = \sqrt[4]{{abcd}}\\
\Rightarrow \frac{{a + b + c + d}}{4} \ge \sqrt[4]{{abcd}}\\
\Rightarrow {\left( {\frac{{a + b + c + d}}{4}} \right)^4} \ge {\left( {\sqrt[4]{{abcd}}} \right)^4}\\
\Leftrightarrow {\left( {\frac{{a + b + c + d}}{4}} \right)^4} \ge abcd
\end{array}\)
Dấu = xảy ra khi
\(\left\{ \begin{array}{l}
a = b\\
c = d\\
\sqrt {ab} = \sqrt {cd}
\end{array} \right. \) \(\Leftrightarrow a = b = c = d\)
Câu 20 trang 112 SGK Đại số 10 nâng cao
Chứng minh rằng:
LG a
Nếu x2 + y2 = 1 thì \(|x + y|\,\, \le \sqrt 2 \)
Phương pháp giải:
Áp dụng bđt 2xy ≤ x2 + y2
Lời giải chi tiết:
Cách 1: Ta có: \({\left( {x - y} \right)^2} \ge 0 \) \(\Leftrightarrow {x^2} + {y^2} - 2xy \ge 0 \) \(\Leftrightarrow {x^2} + {y^2} \ge 2xy\)
Khi đó: (x + y)2 = x2 + y2 + 2xy
≤ x2 + y2 + x2 + y2 = 2
⇒ \(|x + y|\,\, \le \sqrt 2 \)
Dấu = xảy ra khi
\(\left\{ \begin{array}{l}
x = y\\
{x^2} + {y^2} = 1
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x = y\\
2{x^2} = 1
\end{array} \right. \) \( \Leftrightarrow x = y = \pm \frac{1}{{\sqrt 2 }}\)
Cách 2: Áp dụng bất đẳng thức bu- nhi-a-cốp-xki cho hai bộ số (1; 1) và (x, y) ta được:
\(\eqalign{
& {(x + y)^2} = {(x.1 + y.1)^2} \cr &\le ({x^2} + {y^2})({1^2} + {1^2}) = 2 \cr
& \Rightarrow |x + y| \le \sqrt 2 \cr} \)
LG b
Nếu 4x – 3y = 15 thì x2 + y2 ≥ 9
Phương pháp giải:
Áp dụng bđt Bunhia:
\({\left( {ax + by} \right)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\)
Lời giải chi tiết:
Áp dụng bất đẳng thức Bu- nhi-a – cốp- xki cho bộ hai số (4; -3) và ( x; y) ta được:
\(\begin{array}{l}{\left( {4x - 3y} \right)^2} \le \left[ {{4^2} + {{\left( { - 3} \right)}^2}} \right]\left( {{x^2} + {y^2}} \right)\\ \Leftrightarrow {15^2} \le 25\left( {{x^2} + {y^2}} \right)\\ \Leftrightarrow 9 \le {x^2} + {y^2}\\ \Rightarrow {x^2} + {y^2} \ge 9\end{array}\)
Dấu đẳng thức xảy ra khi và chỉ khi:
\(\left\{ \begin{array}{l}
\frac{x}{4} = \frac{y}{{ - 3}}\\
4x - 3y = 15
\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = \frac{{12}}{5}\\y = - \frac{9}{5}\end{array} \right.\)
Cách khác:
Vì 4x – 3y = 15 \( \Rightarrow y = {4 \over 3}x - 5\)
Do đó:
\(\eqalign{
& {x^2} + {y^2} = {x^2} + {({4 \over 3}x - 5)^2} \cr&= {x^2} + {{16} \over 9}{x^2} - {{40} \over 3}x + 25 \cr
& ={{25} \over 9}{x^2} - {{40} \over 3}x + 25 \cr &= {({5 \over 3}x - 4)^2} + 9 \ge 9 \cr} \)
Được cập nhật: 4 tháng 4 lúc 2:05:30 | Lượt xem: 449




